《数电》学习-第二章-逻辑代数

目录

正文

一.逻辑代数的基本运算

1.概述

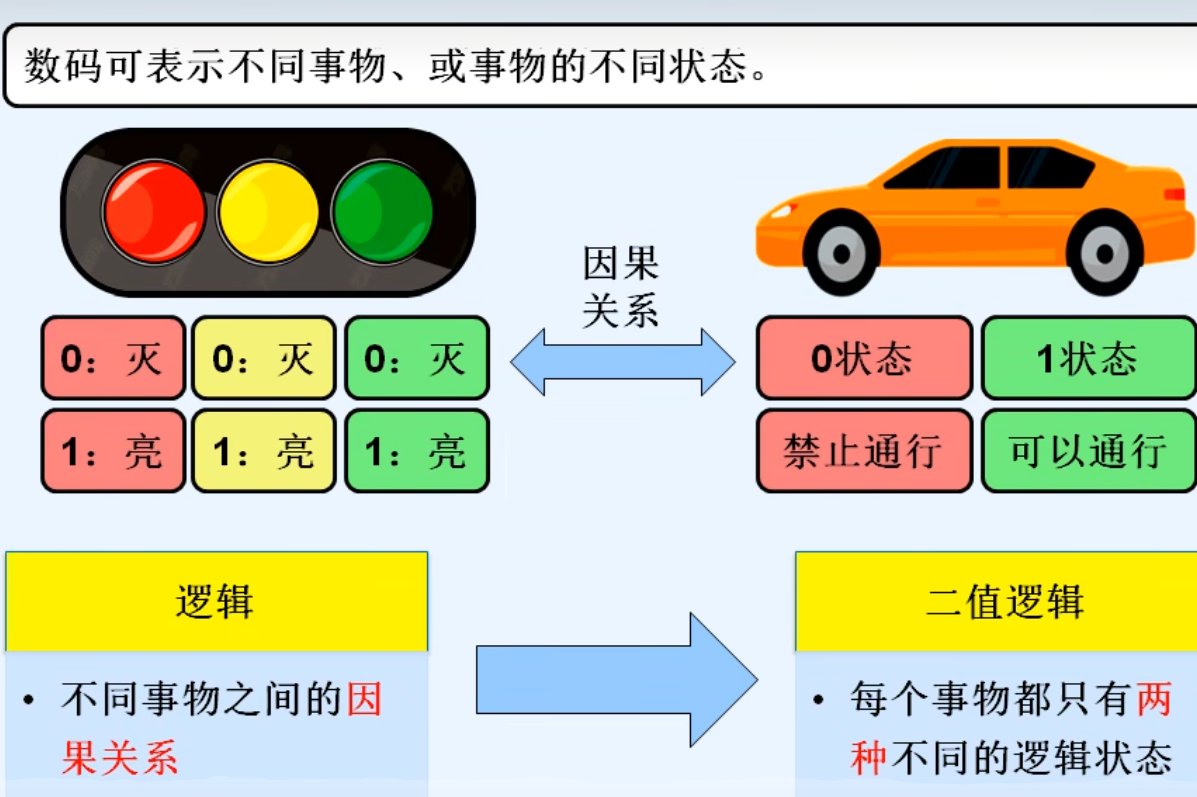
image-20240401215114207

image-20240401215150134

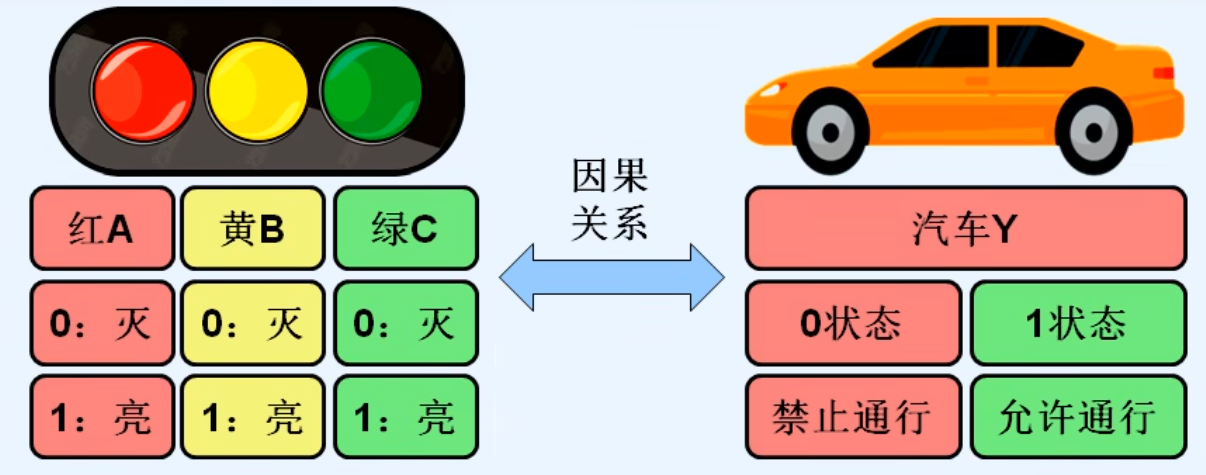
image-20240401215239389

image-20240401215317578

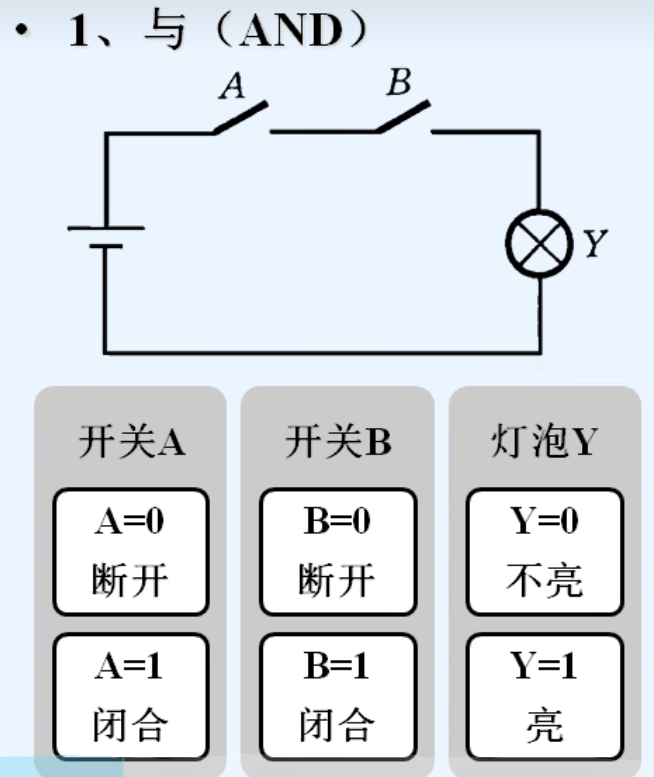
2.逻辑代数的三种基本运算

image-20240401215438476

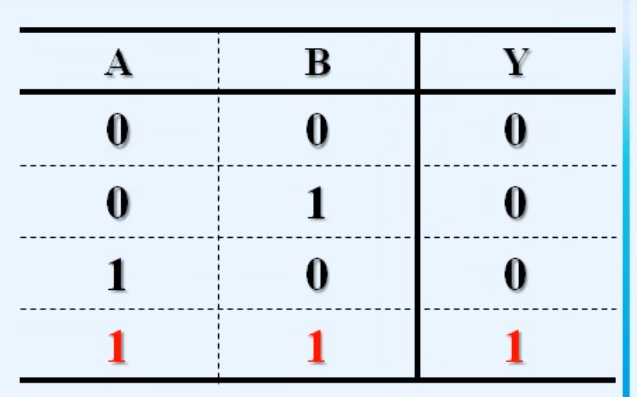
image-20240401215503033

image-20240401215532251

image-20240401215543735

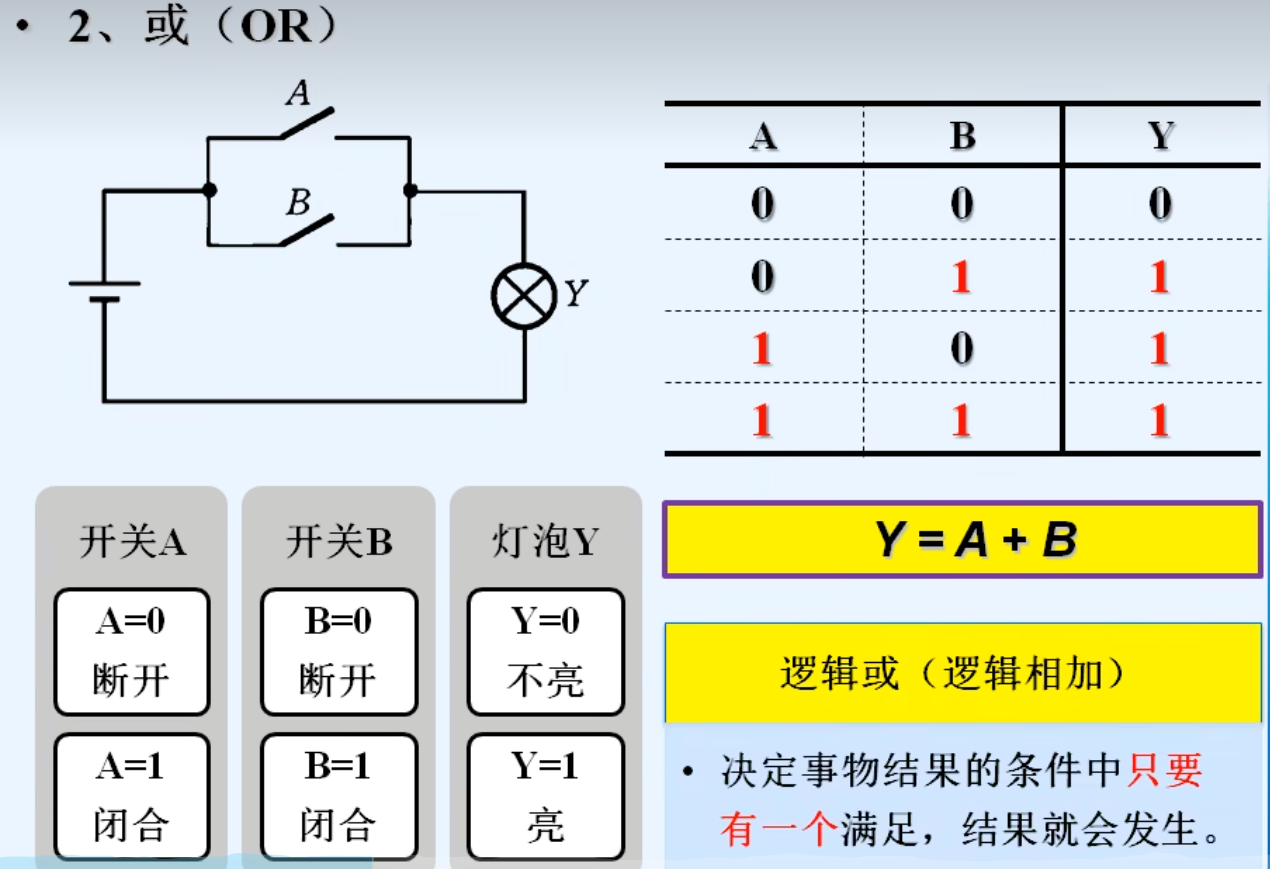
image-20240401215715077

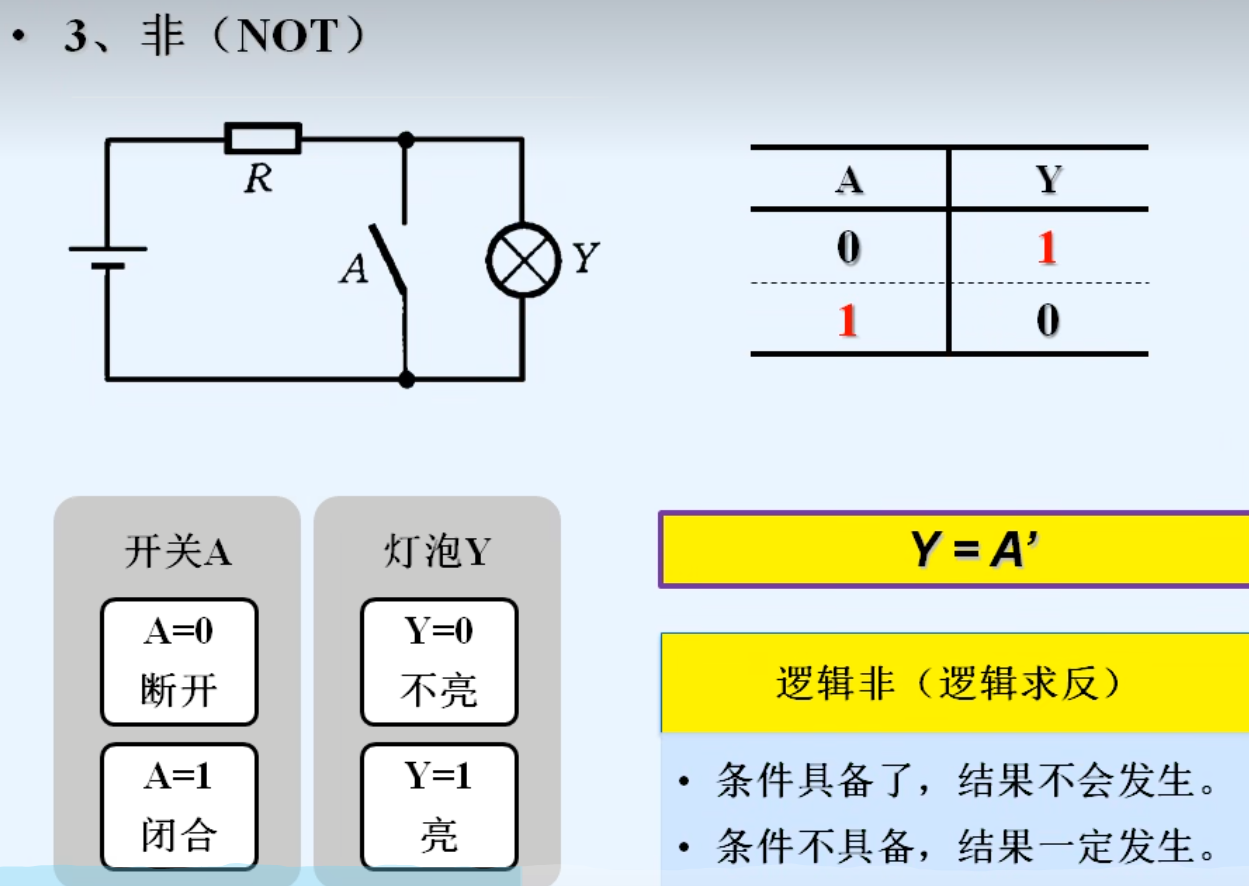
image-20240401215852705

image-20240401215948983

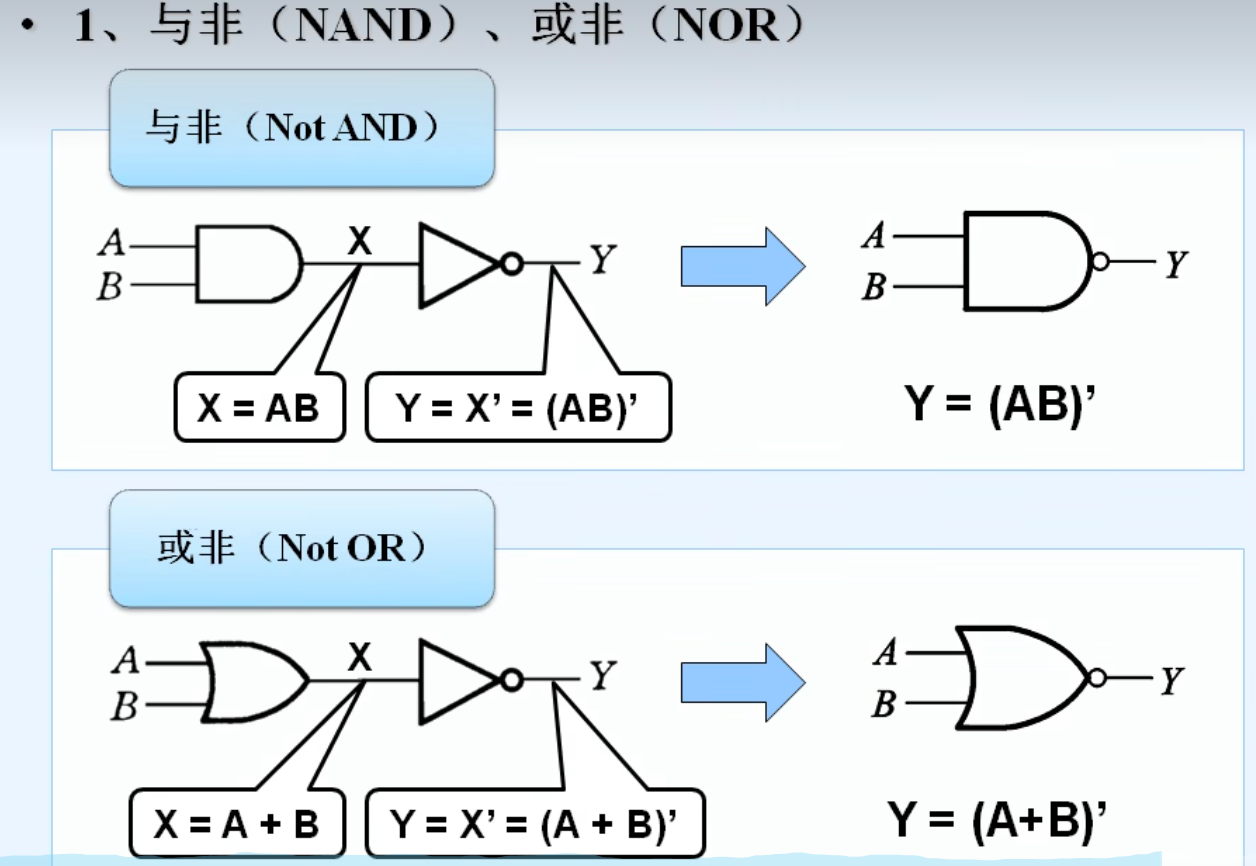
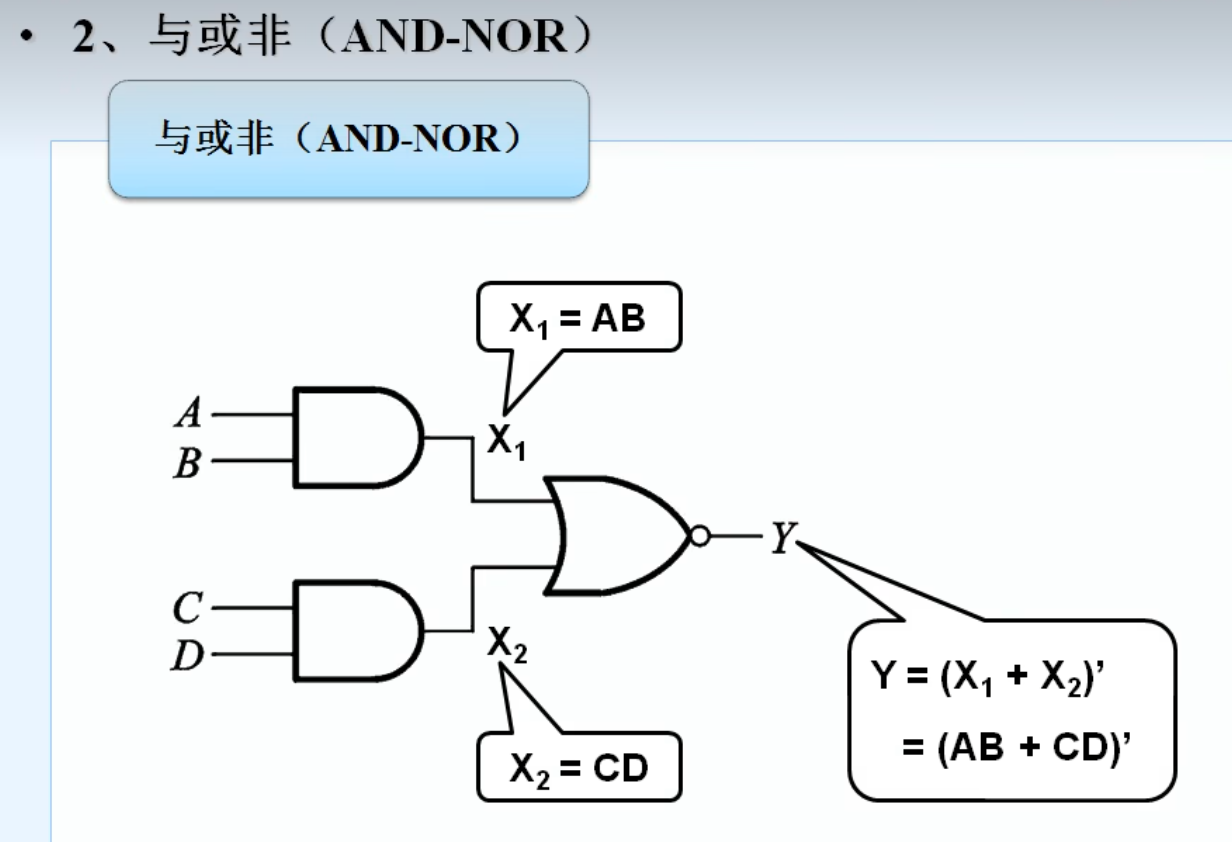
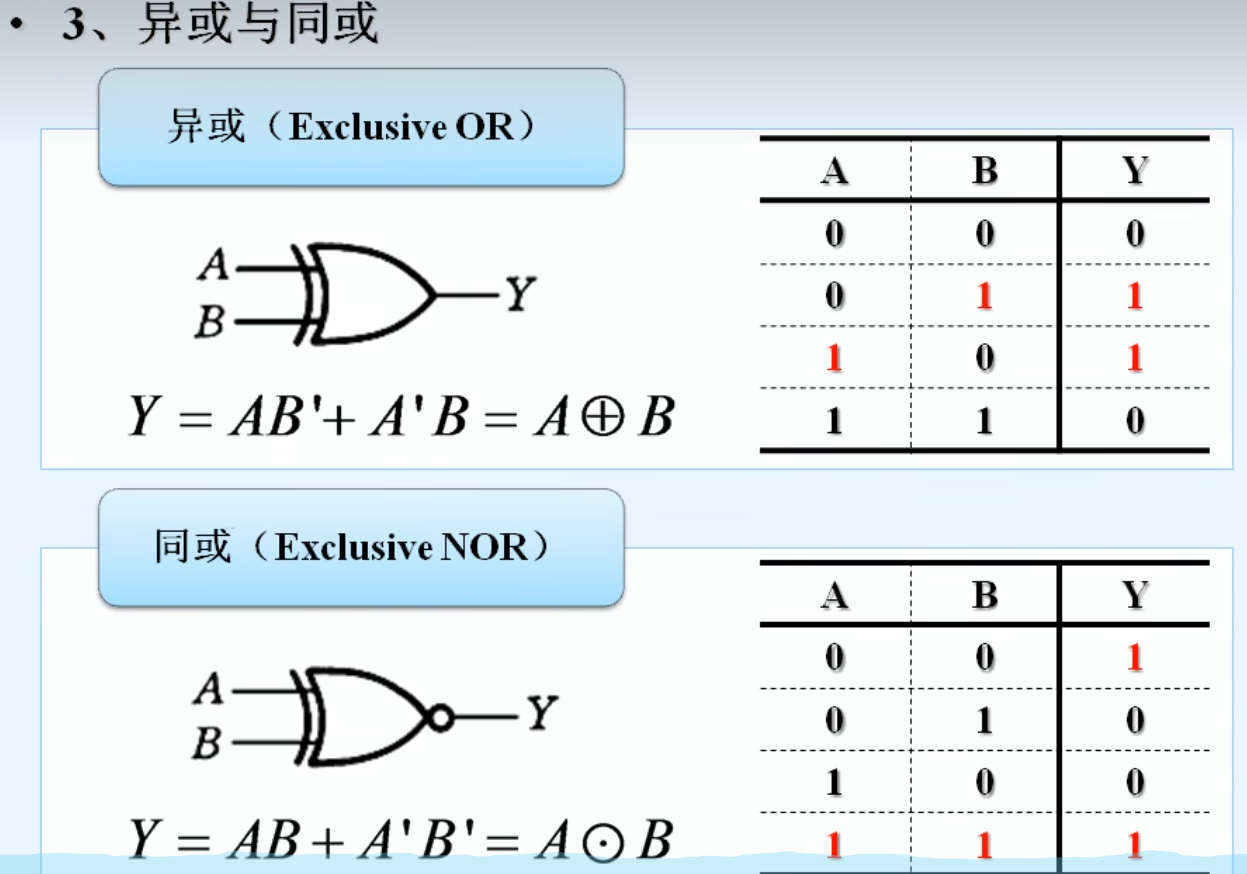
3.常见的复合逻辑运算

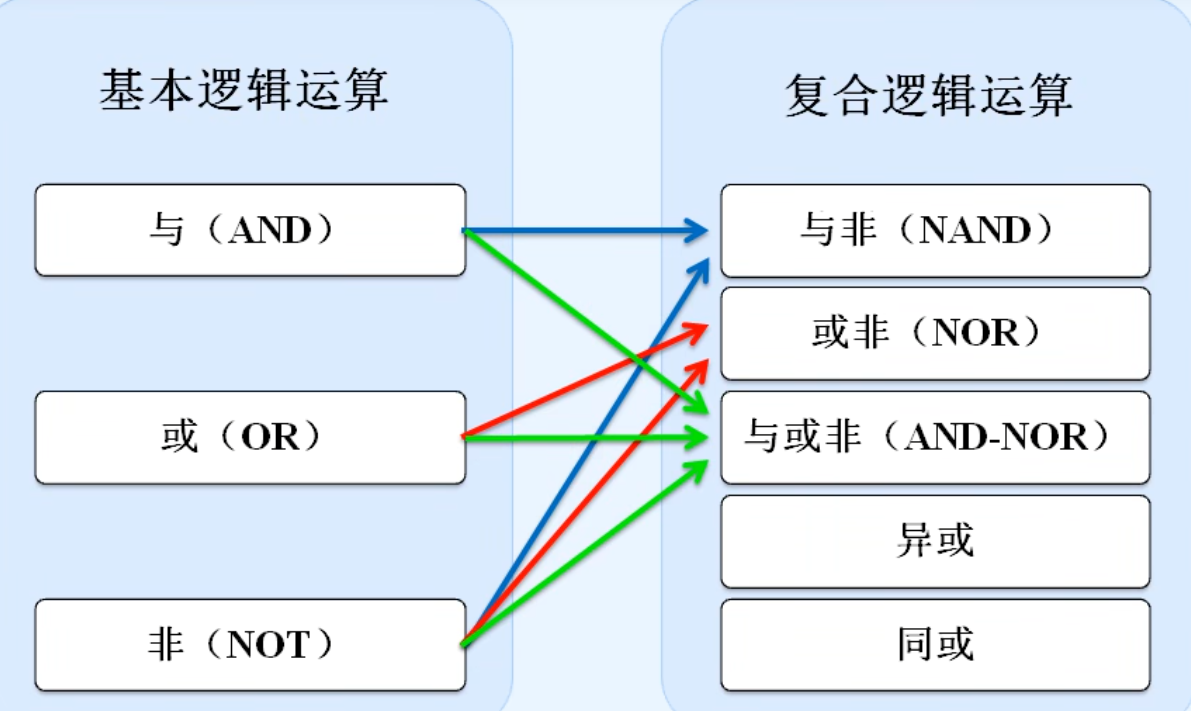
image-20240401220238787

image-20240401220526253

image-20240401220652570

image-20240401220900054

image-20240401220926026

二.逻辑代数的基本公式和常用公式

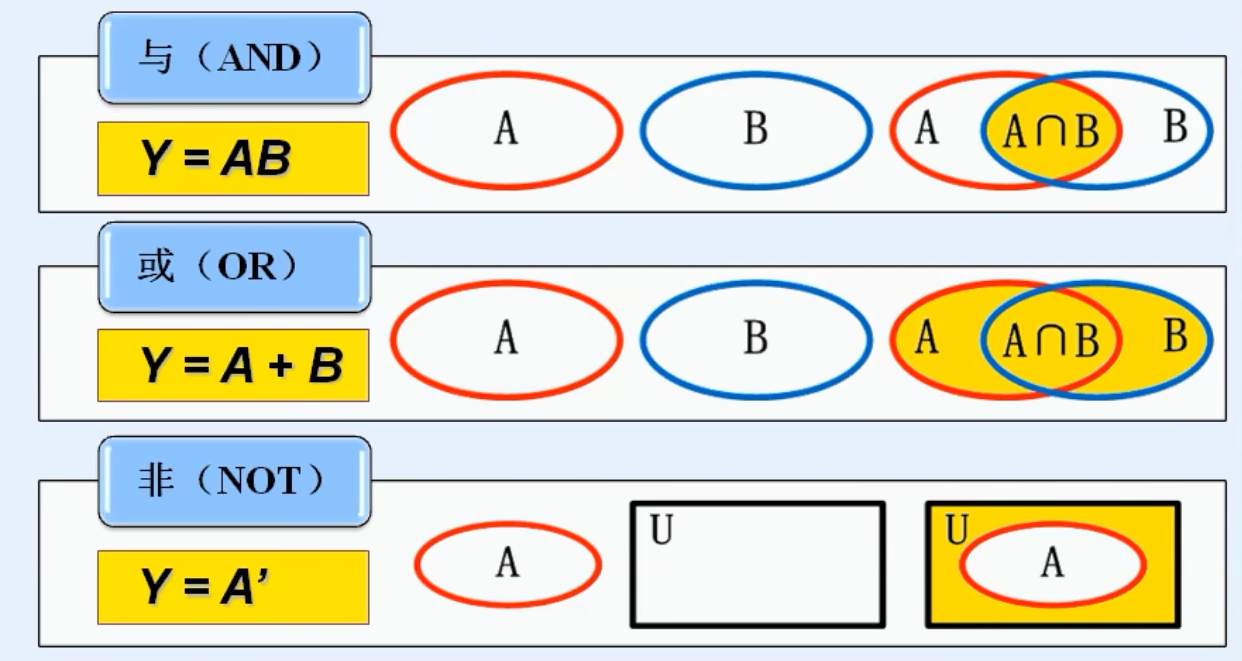
1.逻辑代数与集合

image-20240401221157964

2.常量公式

image-20240401221301864

3.常量与变量公式

image-20240401221506191

4.单变量公式

image-20240401221725725

5.双变量公式

image-20240401222005901

6.三变量公式

image-20240401222306102

7.常用公式

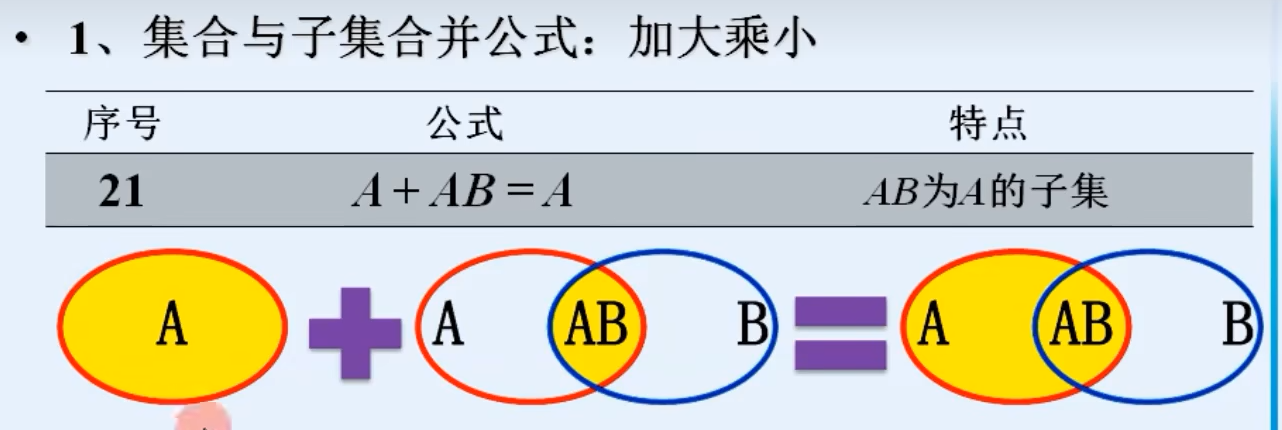
image-20240401222815646

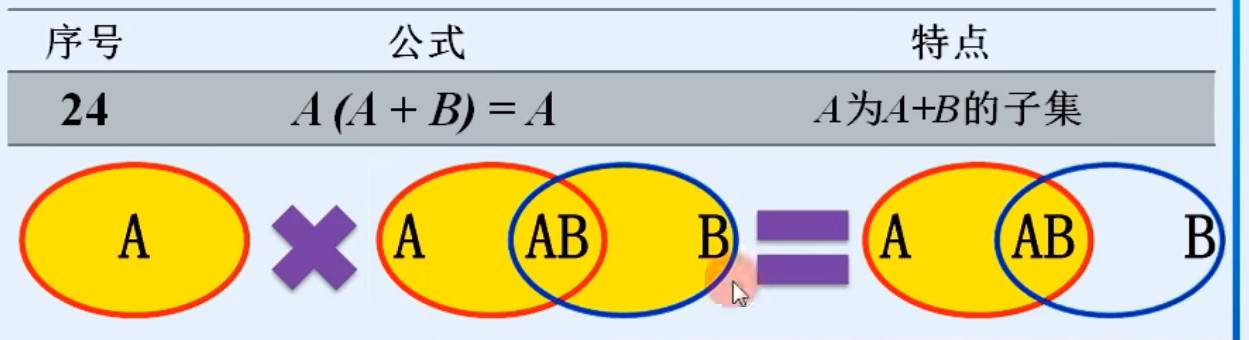
image-20240401222925279

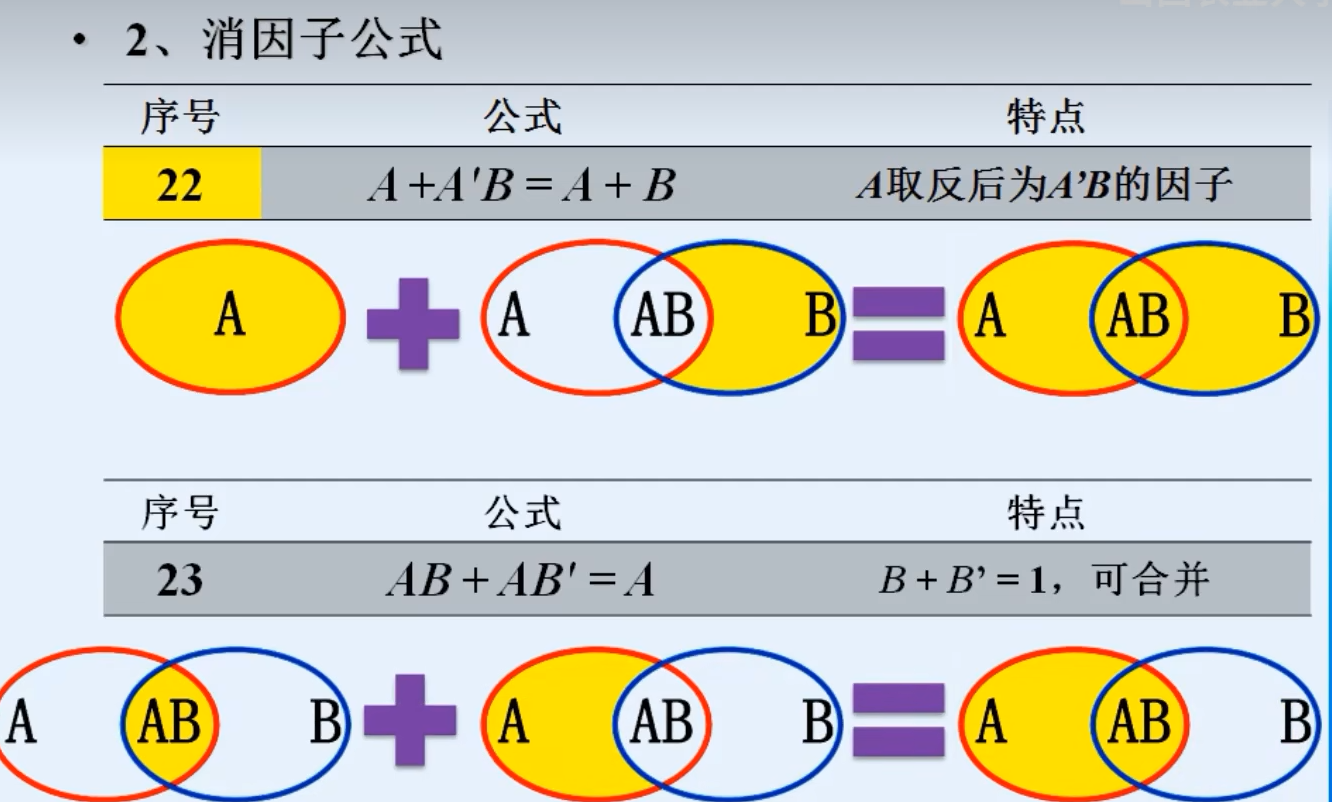
image-20240401223205205

image-20240401223418169

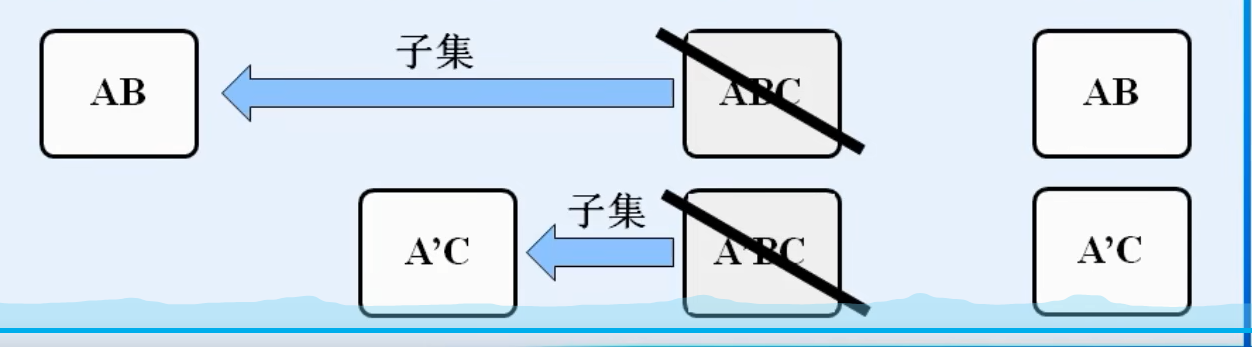
image-20240401223609629

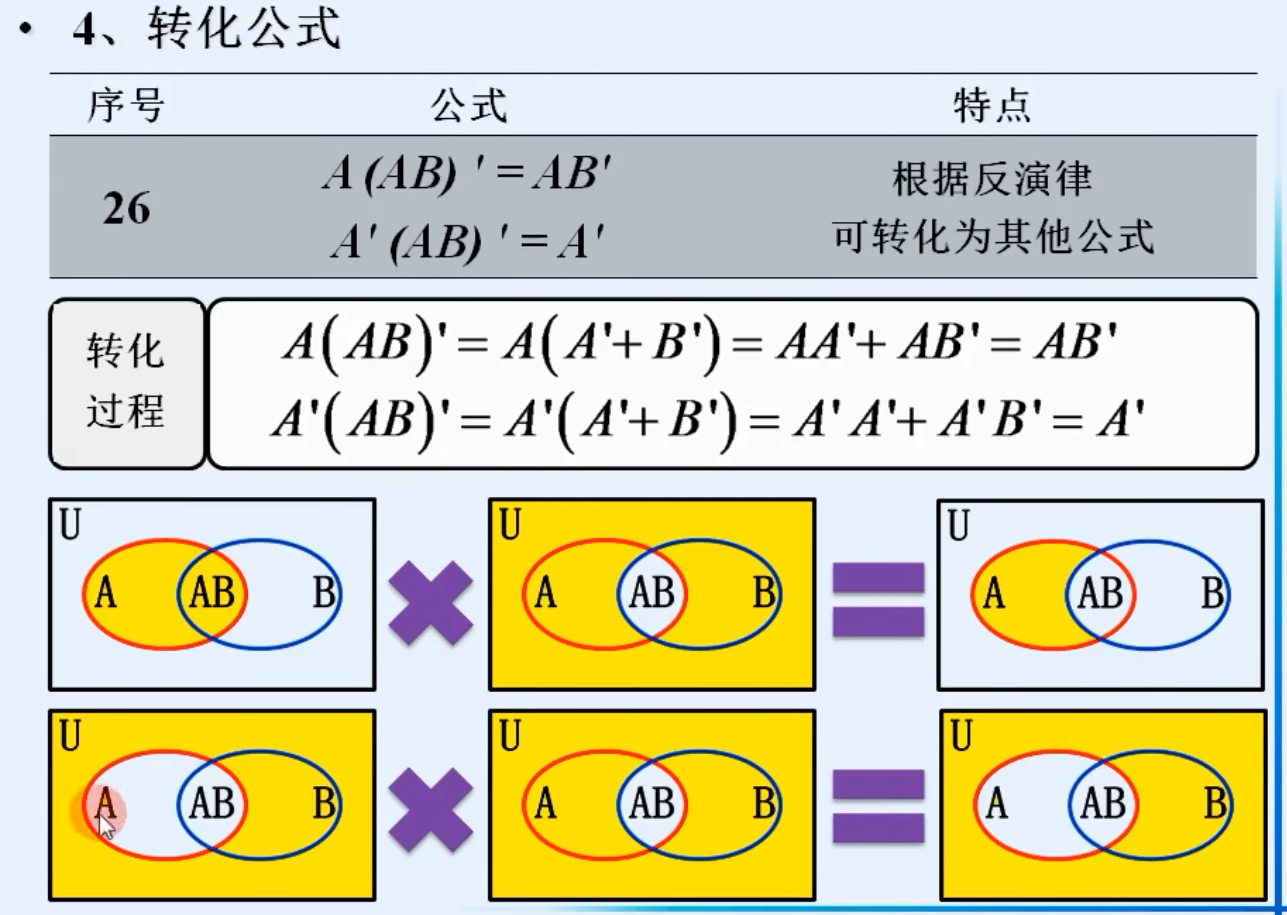
image-20240401223908894

三.逻辑代数的基本定理

1.带入定理（整体替换法）

image-20240401224013621

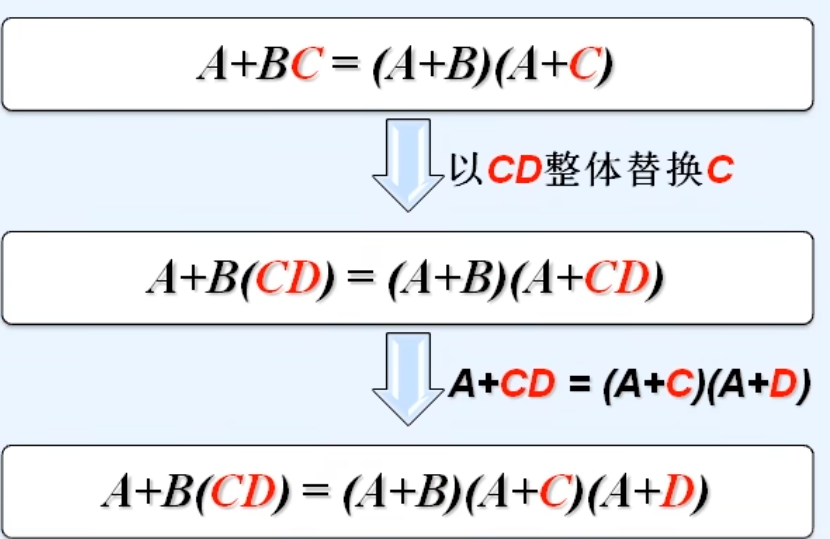
image-20240401224127053

image-20240402212325673

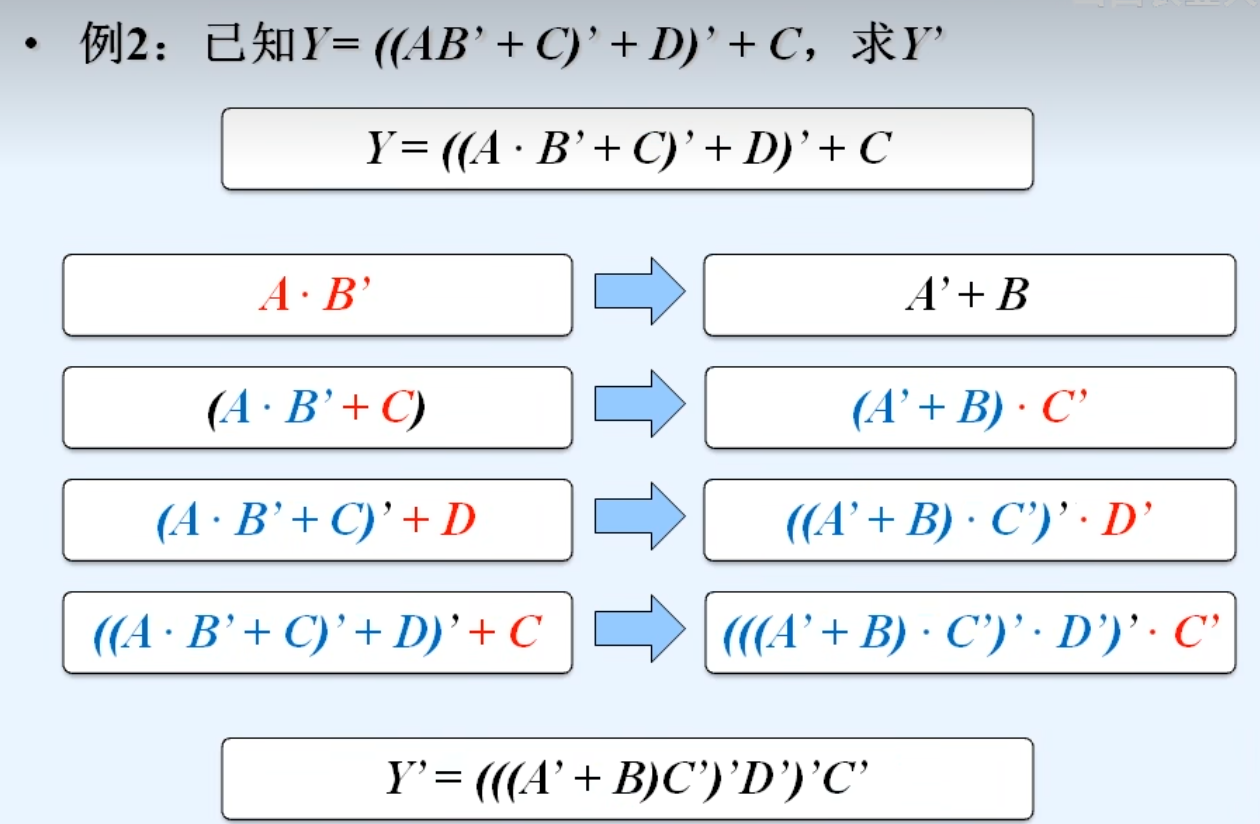
2.反演定理（最重要的定理）

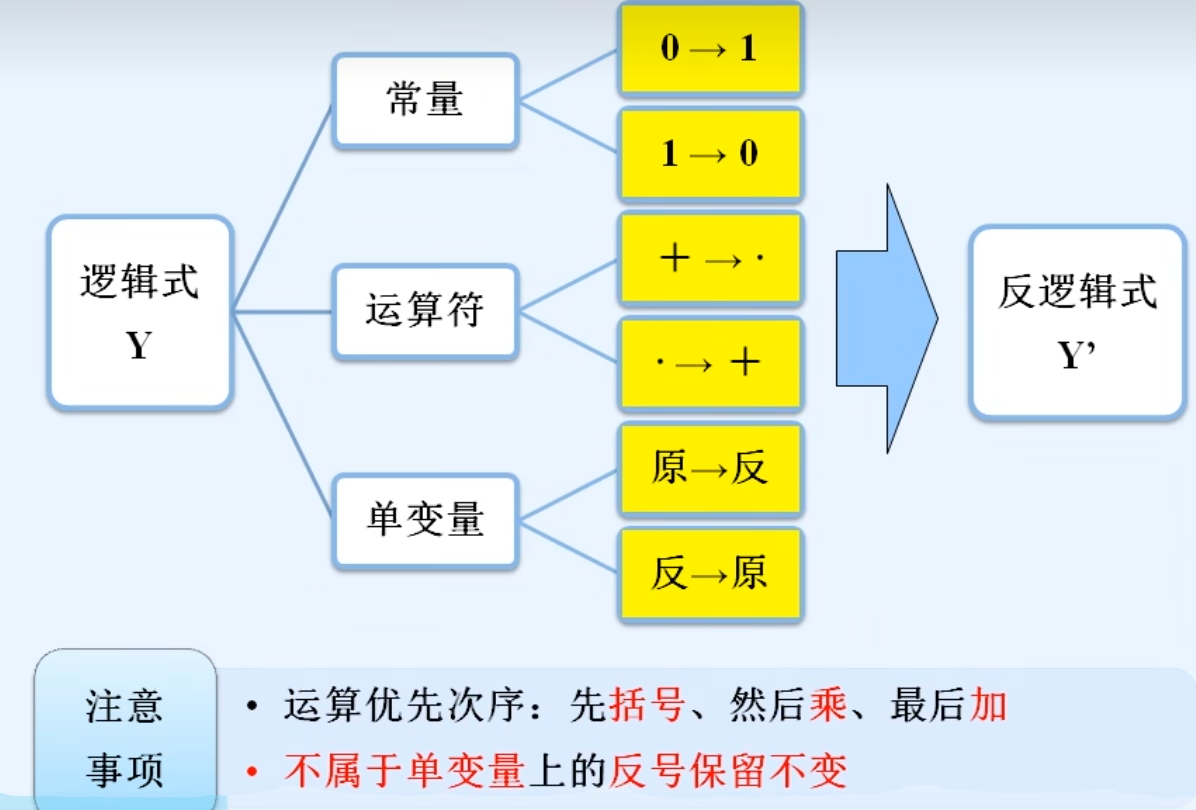
image-20240402212635722

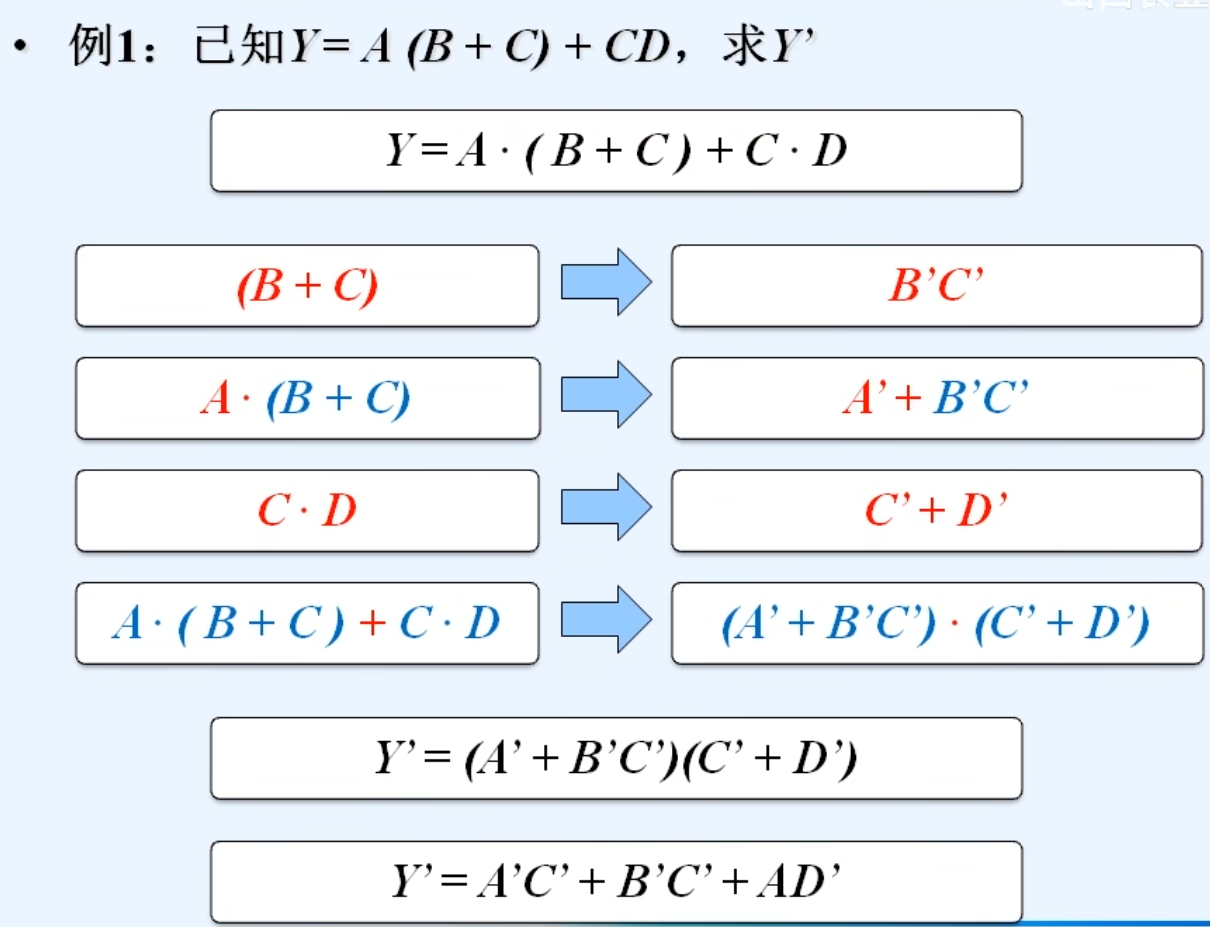
image-20240402212933366

勘误：最后一步是A‘D’而不是AD‘

image-20240402213226926

image-20240402213402933

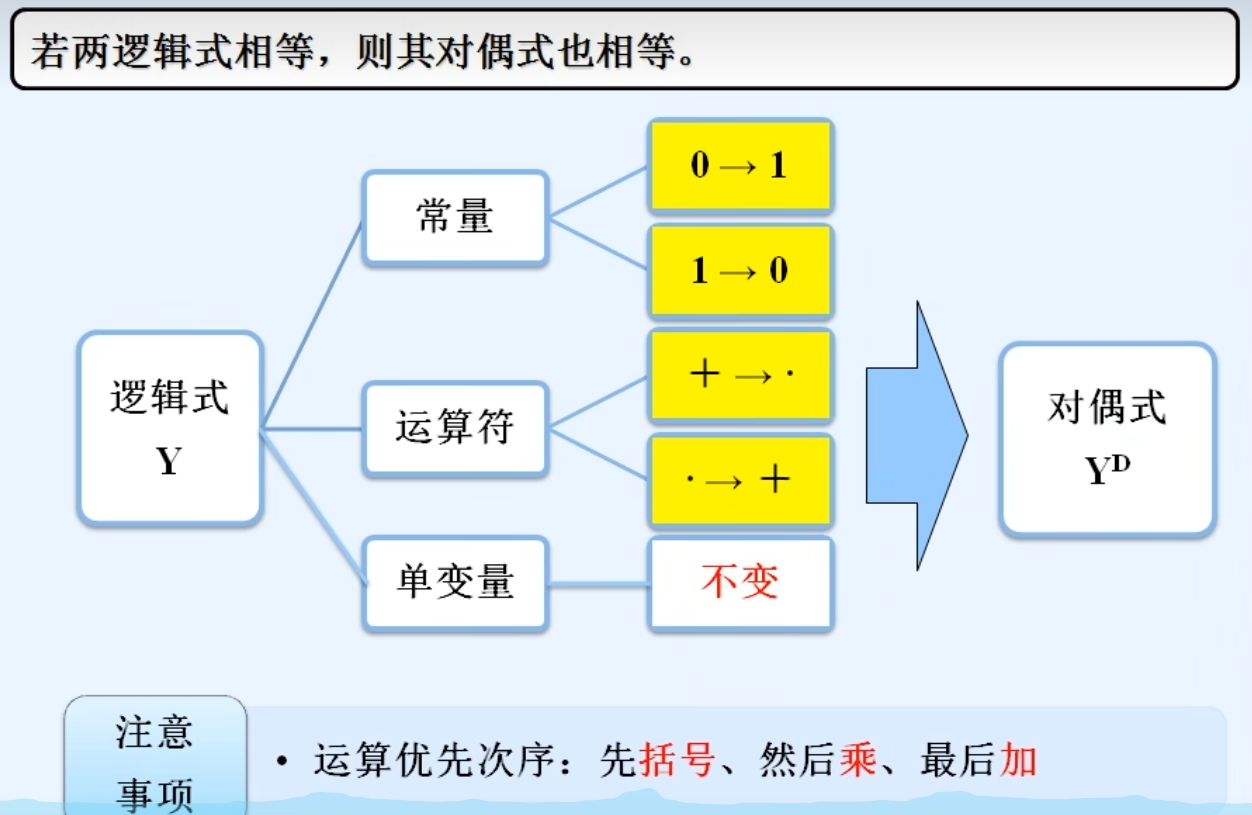
3.对偶定理

image-20240402213546609

image-20240402213755692

四.逻辑函数的描述方法

1.逻辑函数

image-20240402214015306

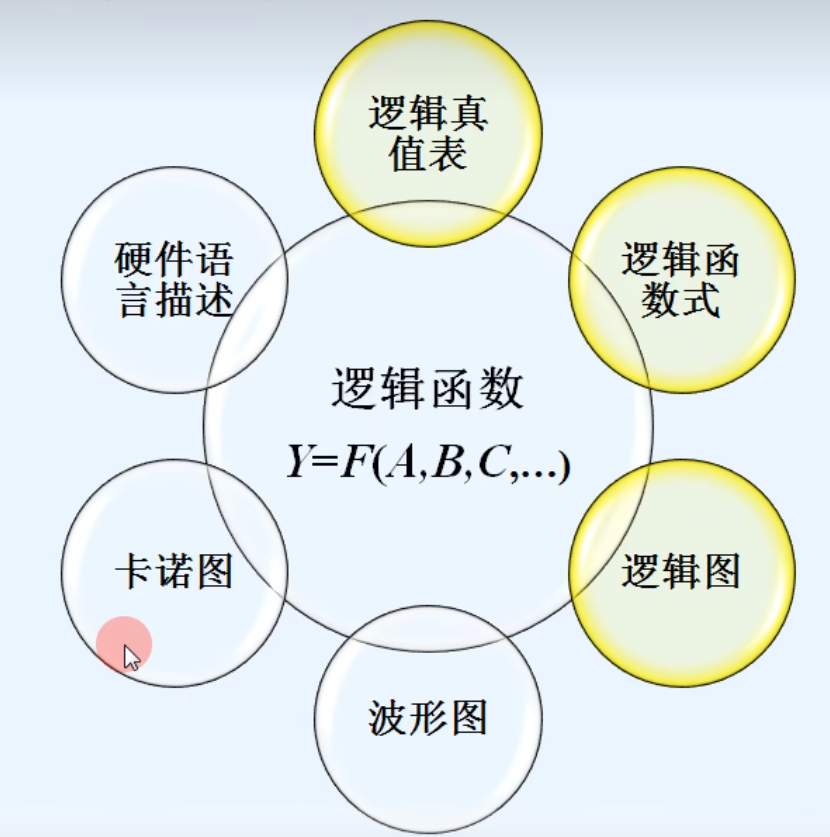
2.逻辑函数的描述方法

image-20240402214108638

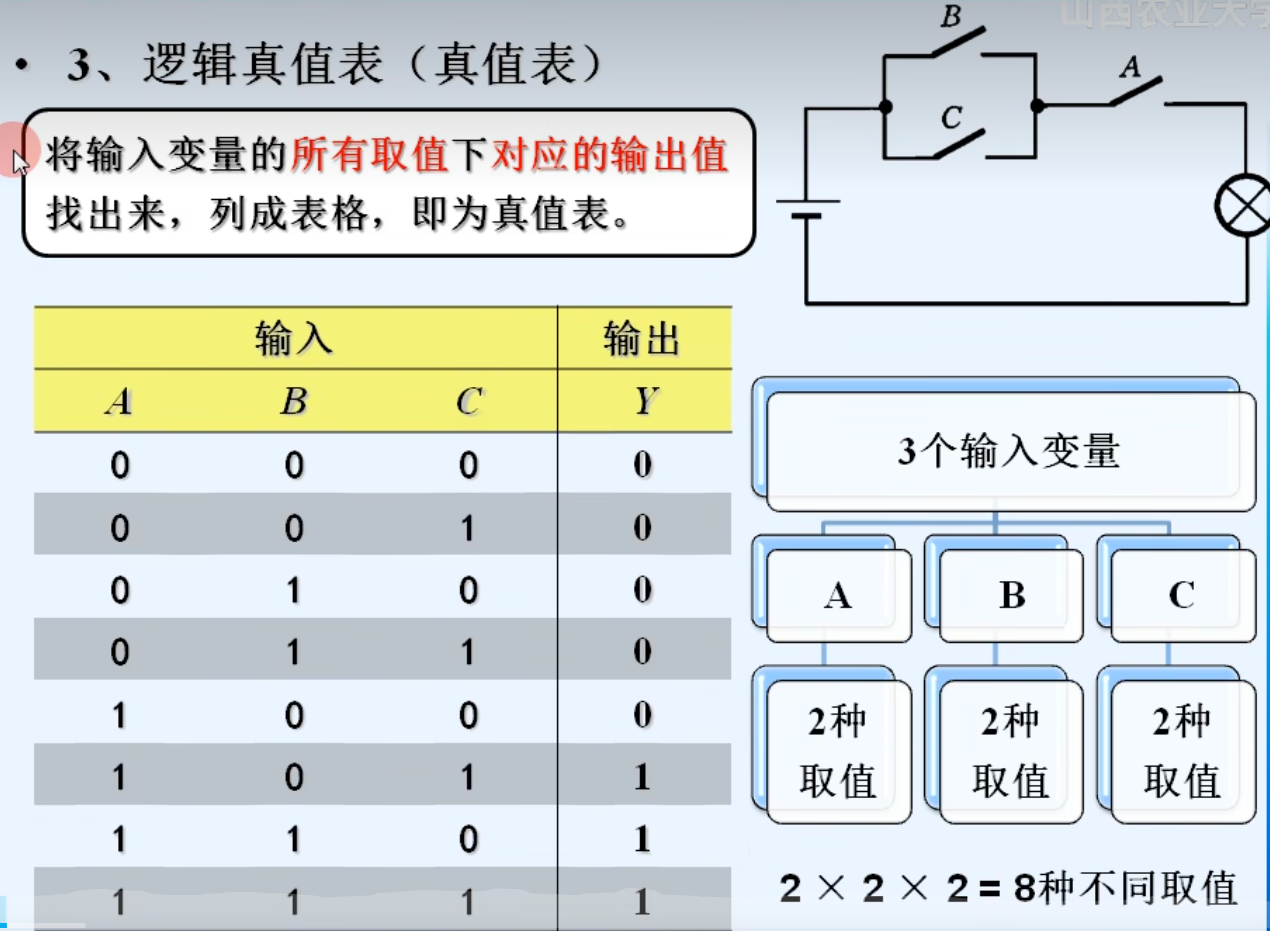
3.逻辑真值表（真值表）

image-20240402214411484

4.逻辑函数式（逻辑式）

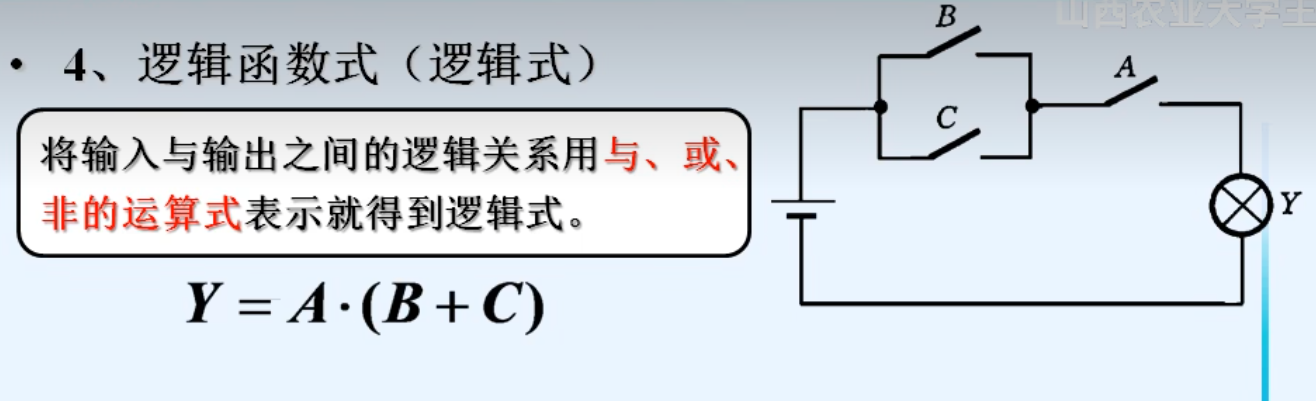
image-20240402214531481

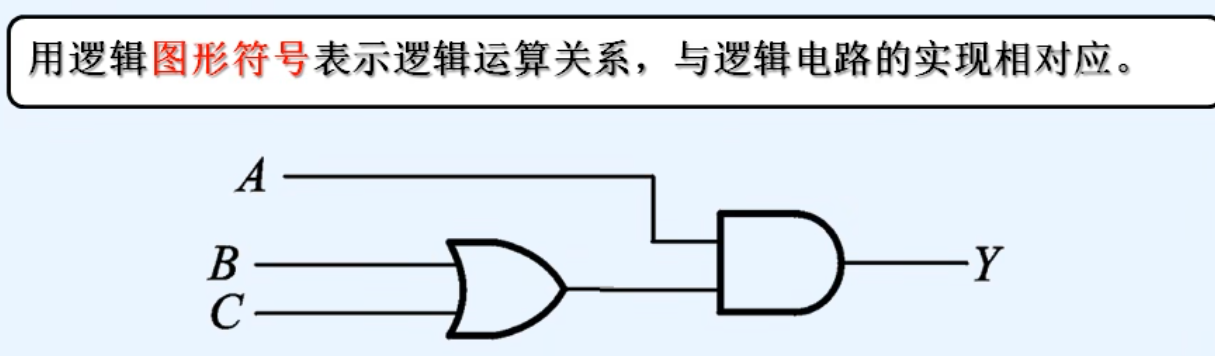
5.逻辑图

image-20240402214623886

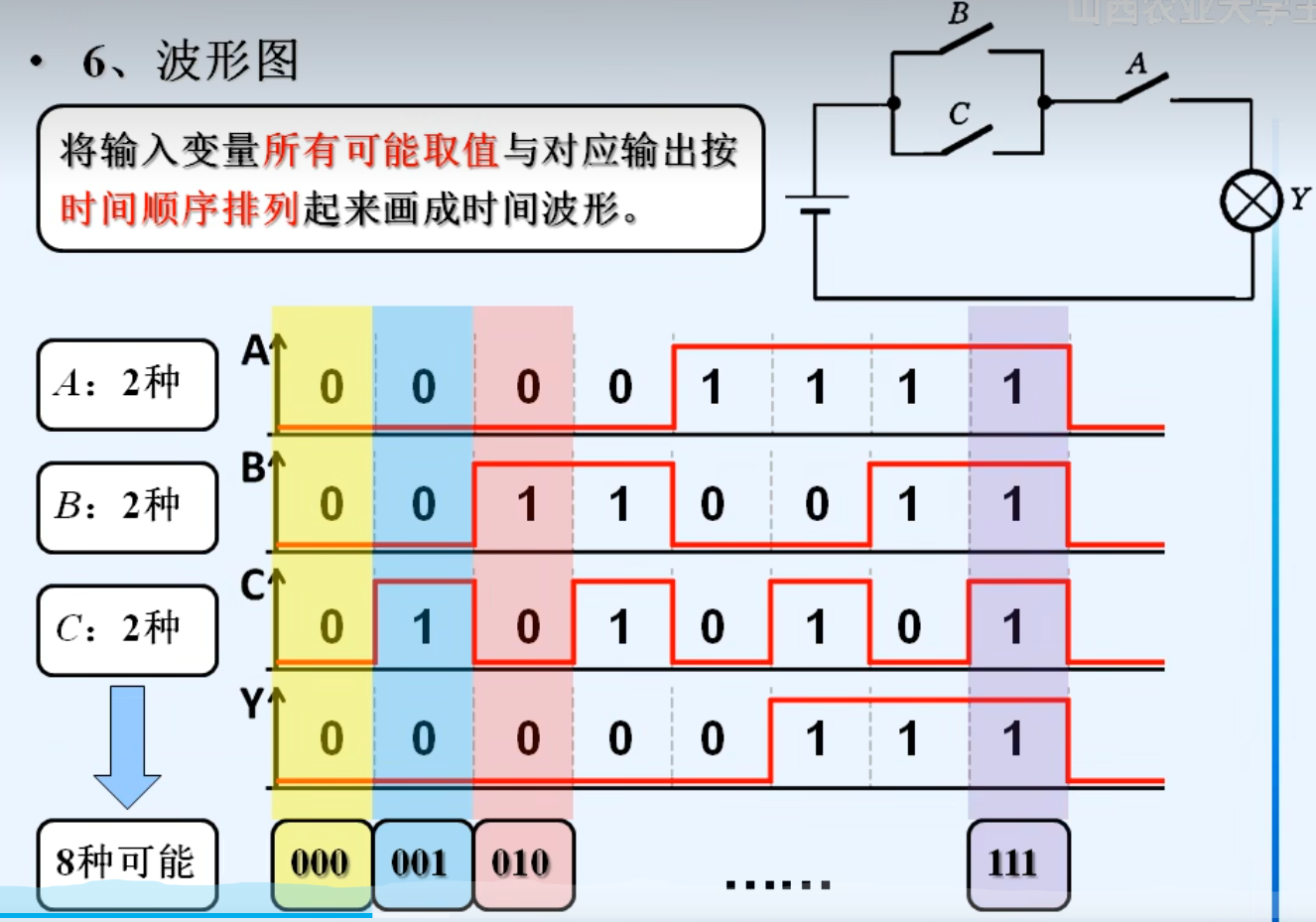
6.波形图

image-20240402214834027

五.逻辑函数描述方法之间的转换

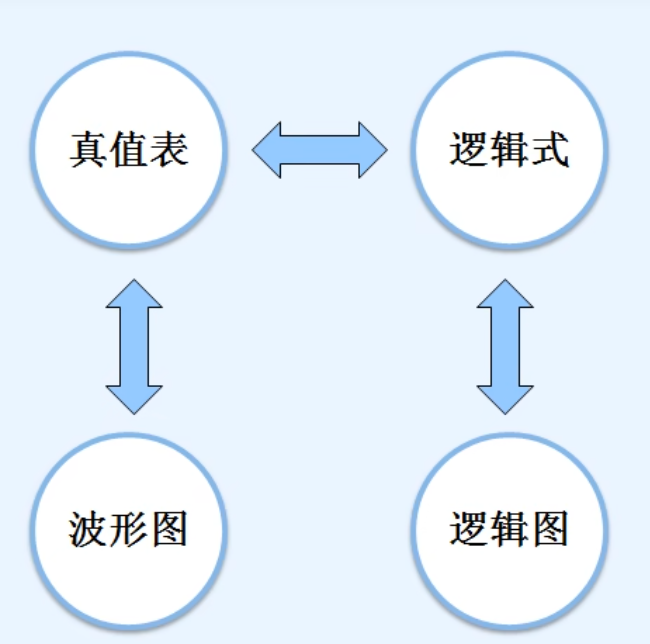
image-20240402214919481

1. 真值表 -》 逻辑式

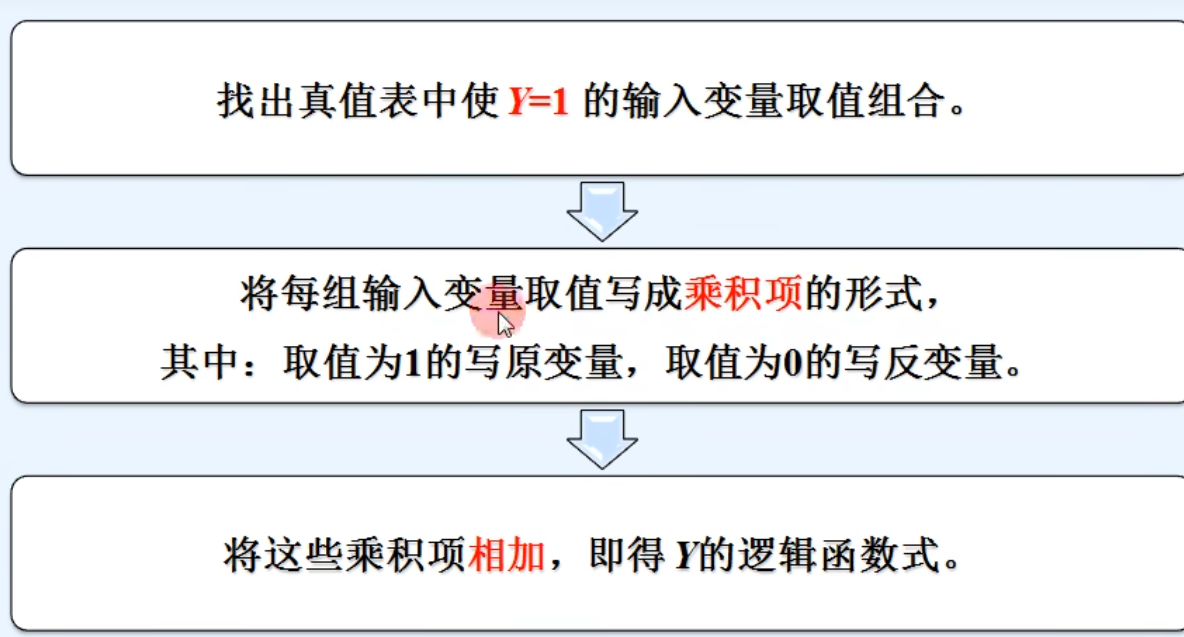
image-20240402215026355

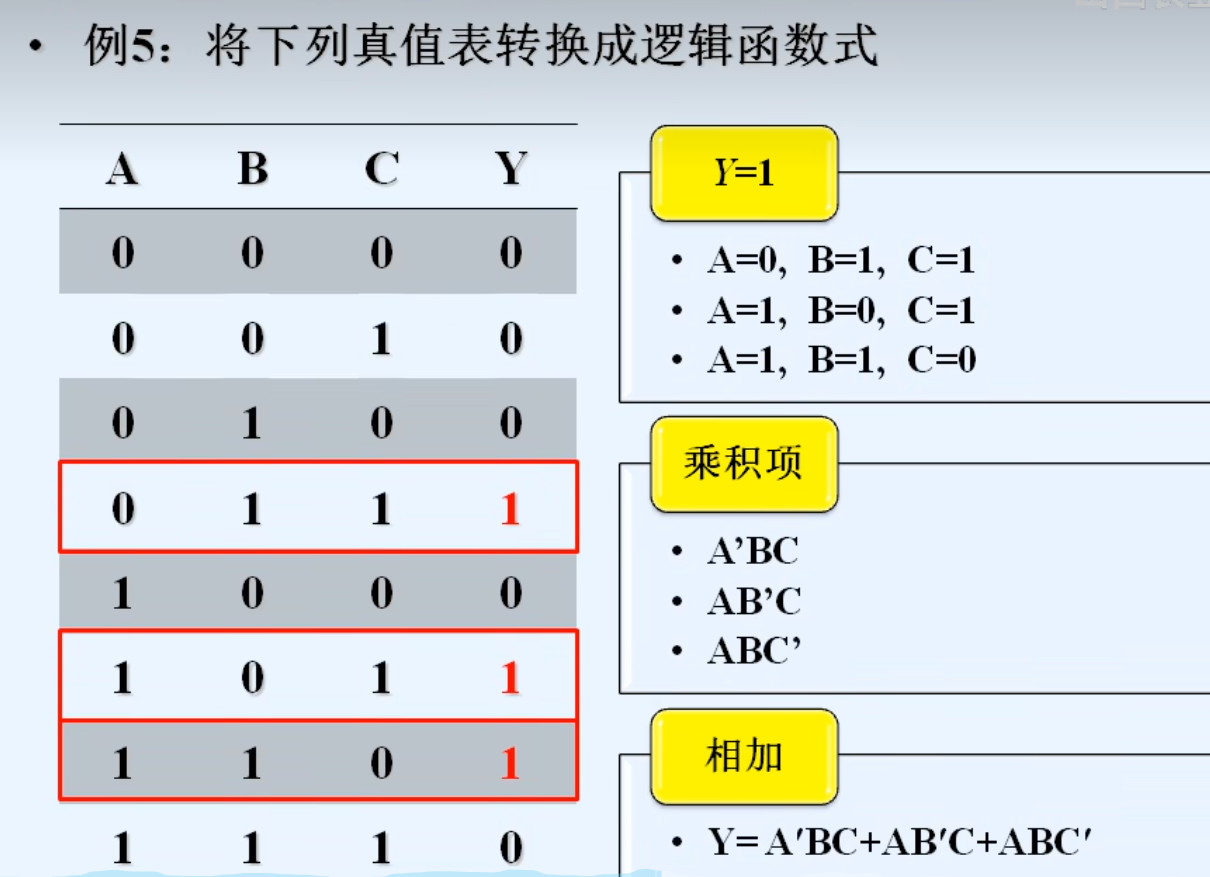
image-20240402220140584

2. 逻辑式 -》 真值表

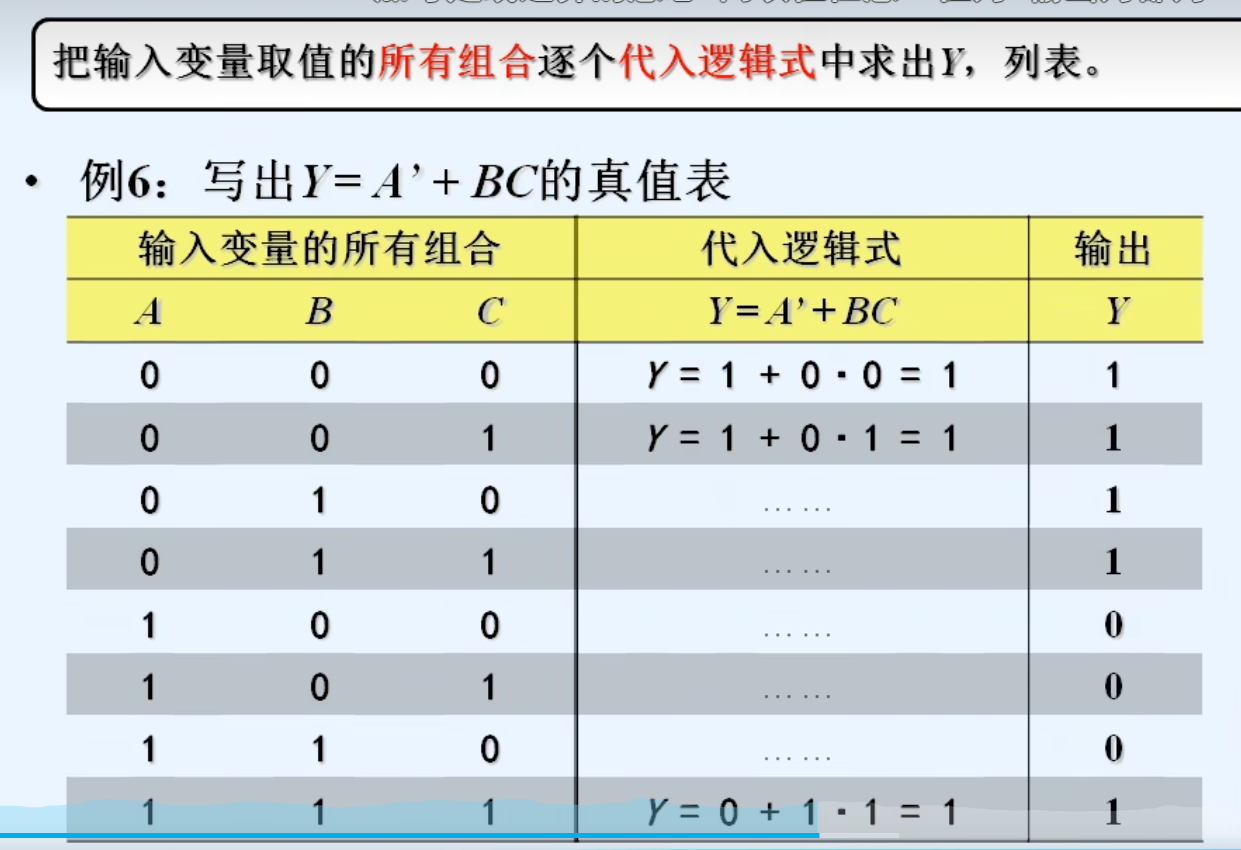
image-20240402220413233

3.逻辑式 -》 逻辑图

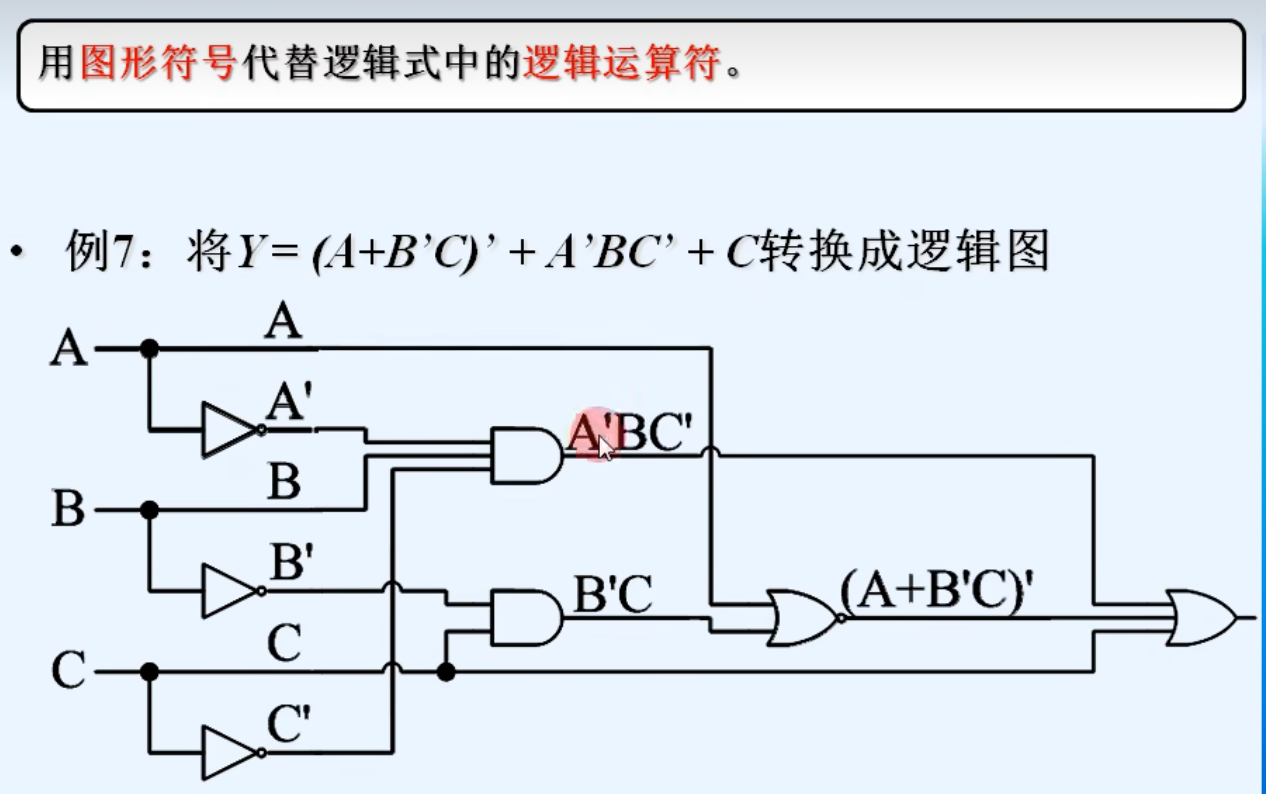
image-20240402222111522

4. 逻辑图 -》 逻辑式

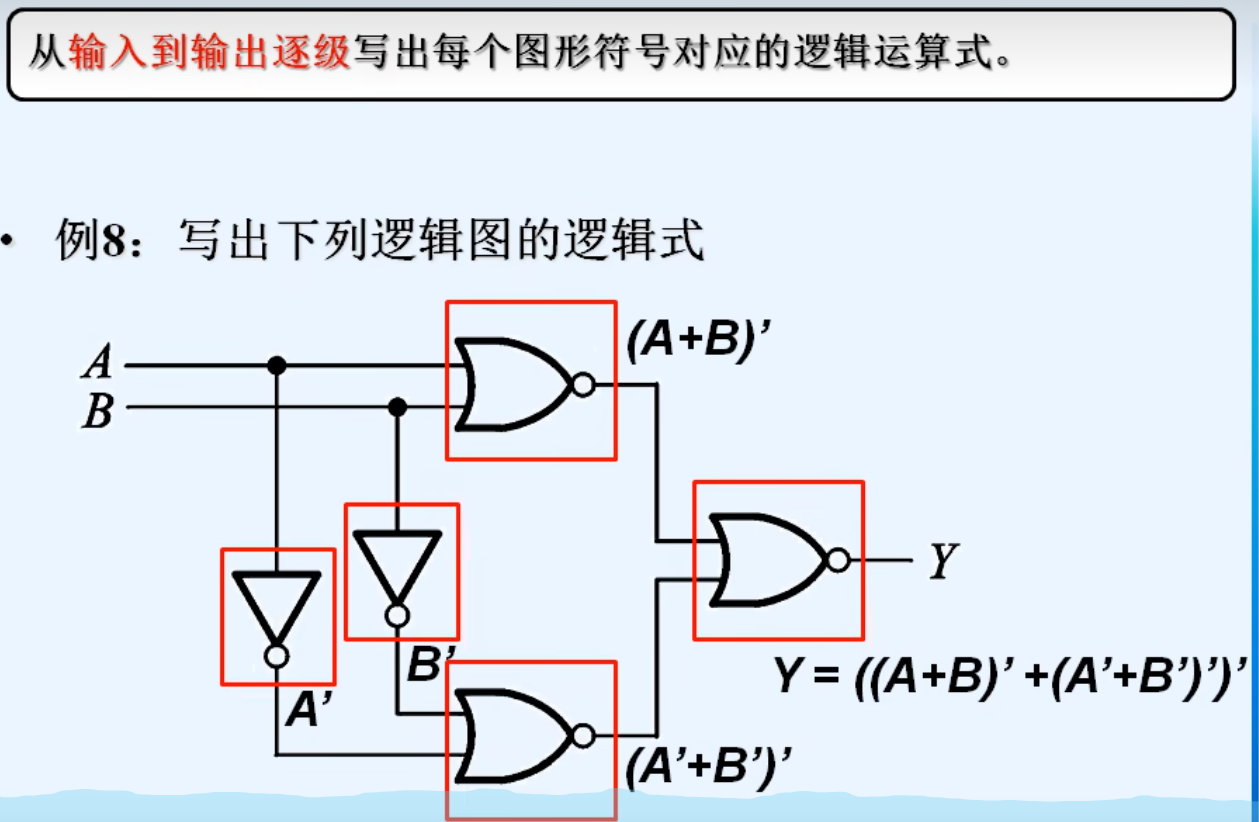
image-20240402222357418

5. 波形图 -》 真值表

image-20240402222700664

六.逻辑函数的两种标准形式

1.最小项与最大项的理解

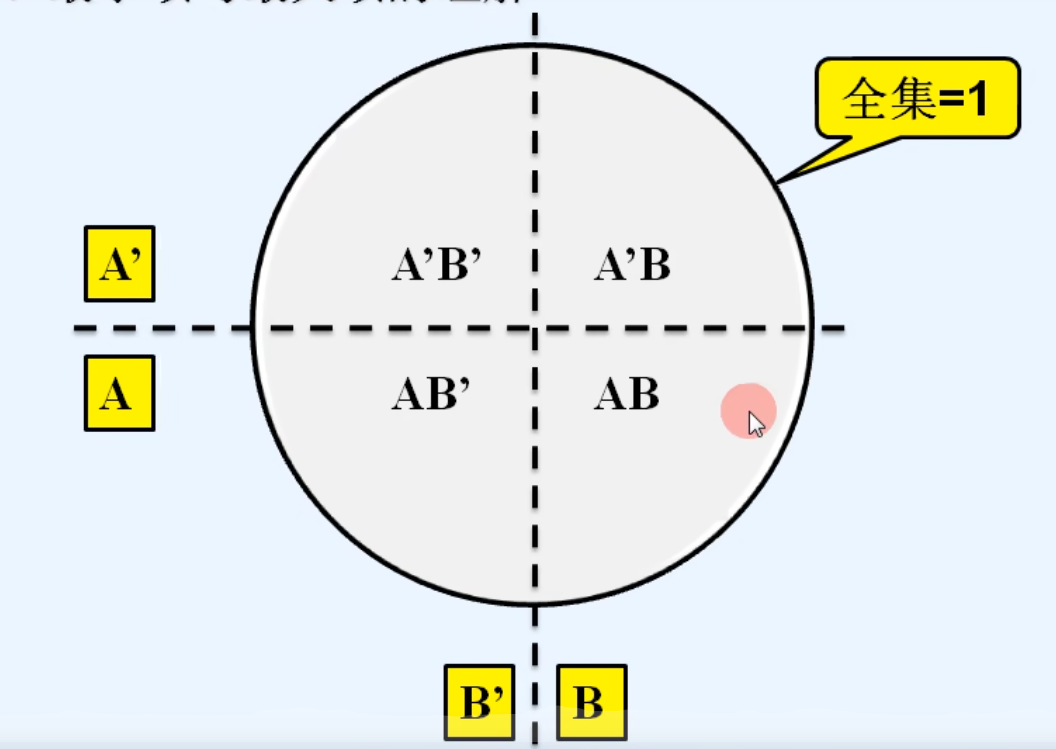
image-20240404205724220

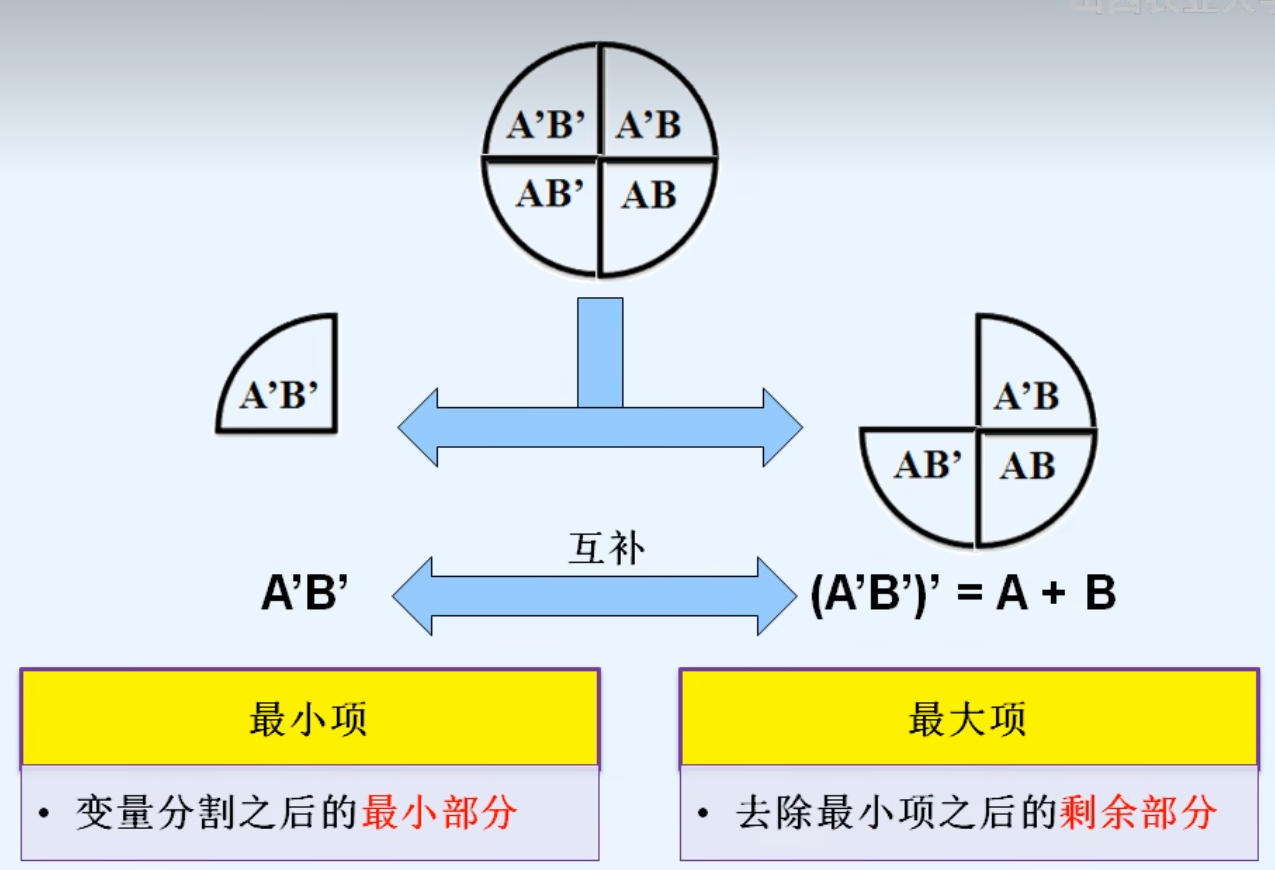
image-20240404205848353

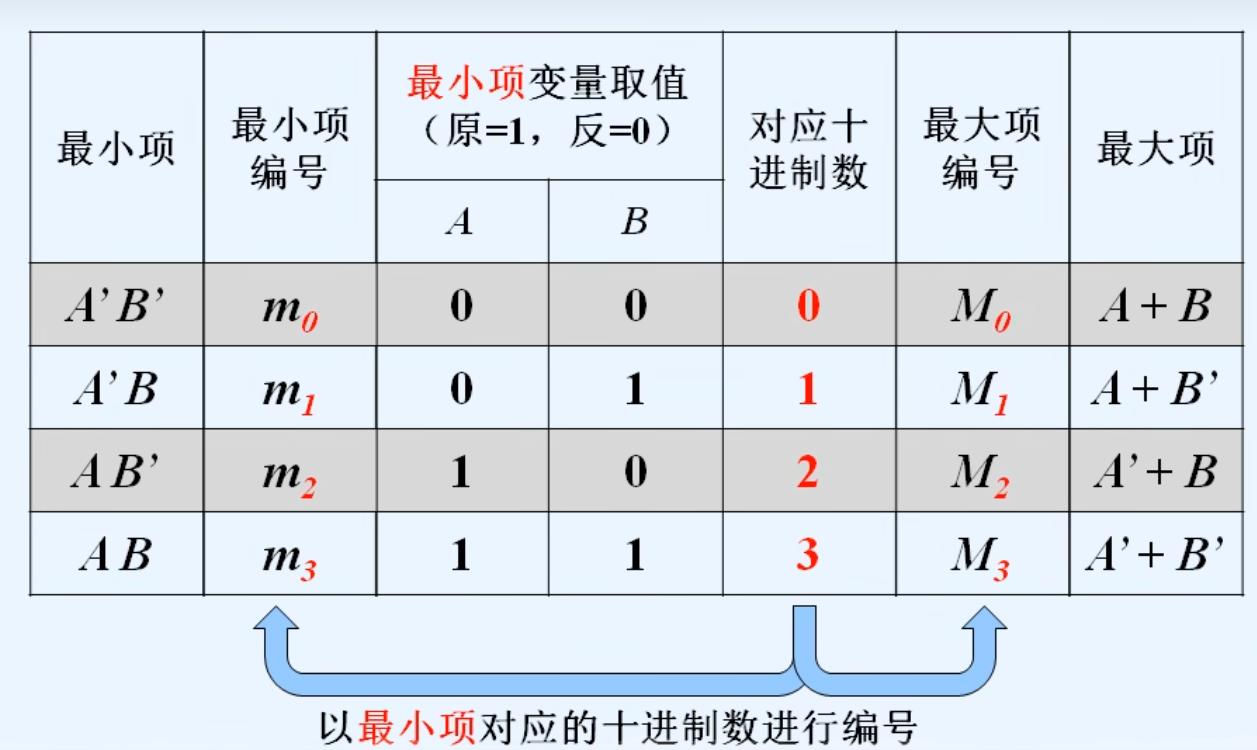
2.两变量的最小项和最大项

image-20240404210210146

3.三变量的最小项与最大项

image-20240404210416041

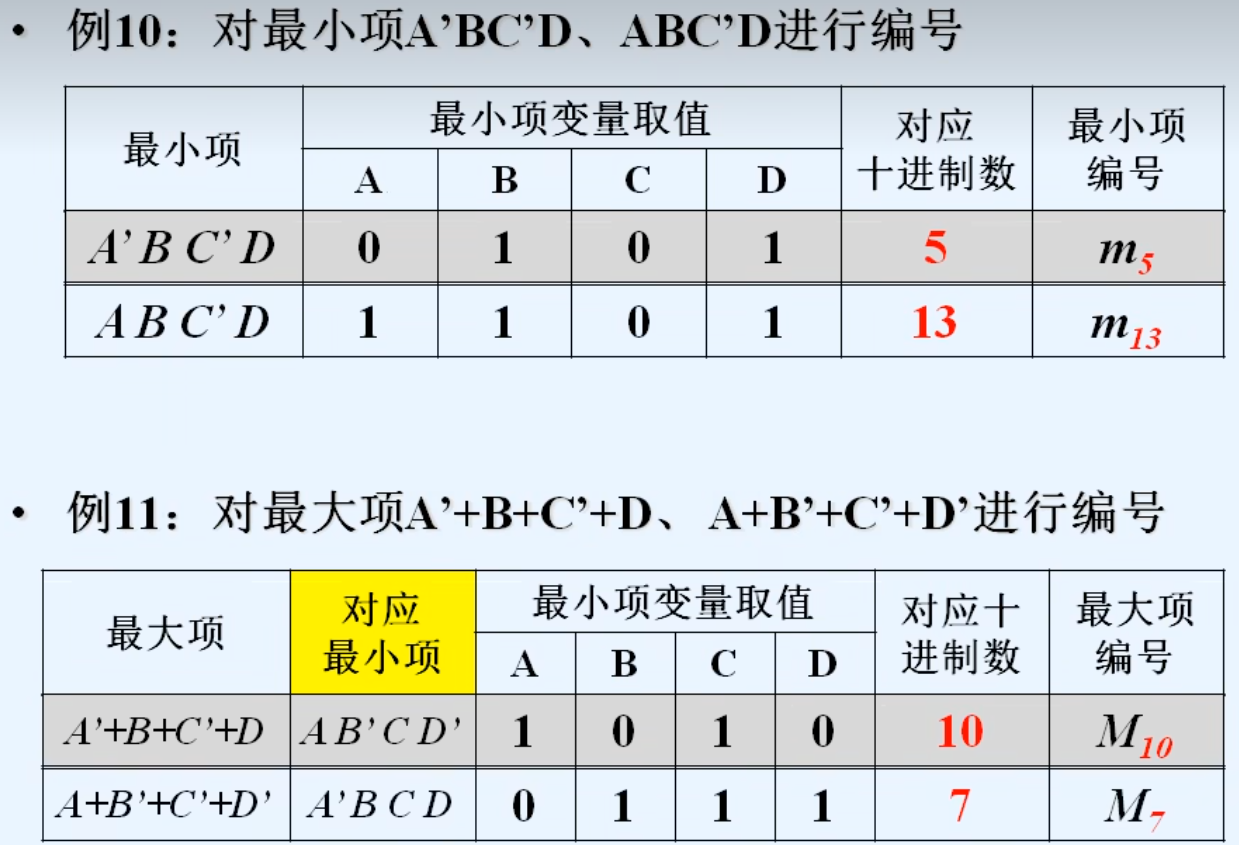
image-20240404210842257

4.最小项与最大项的性质（根据互补性）

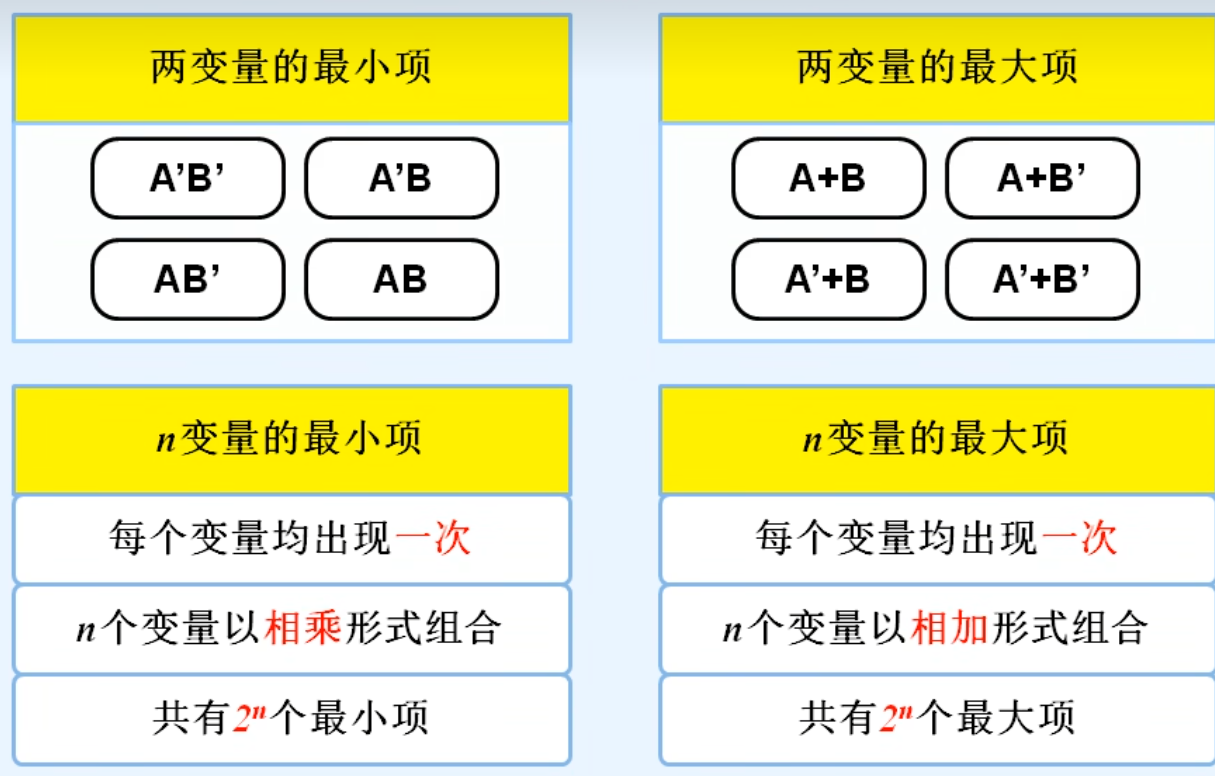
image-20240404211330802

image-20240404211628768

image-20240404211721997

5.逻辑函数的标准形式1——最小项之和形式

image-20240404212214595

image-20240404212452838

结果错了

6.逻辑函数的标准形式2——最大项之积形式

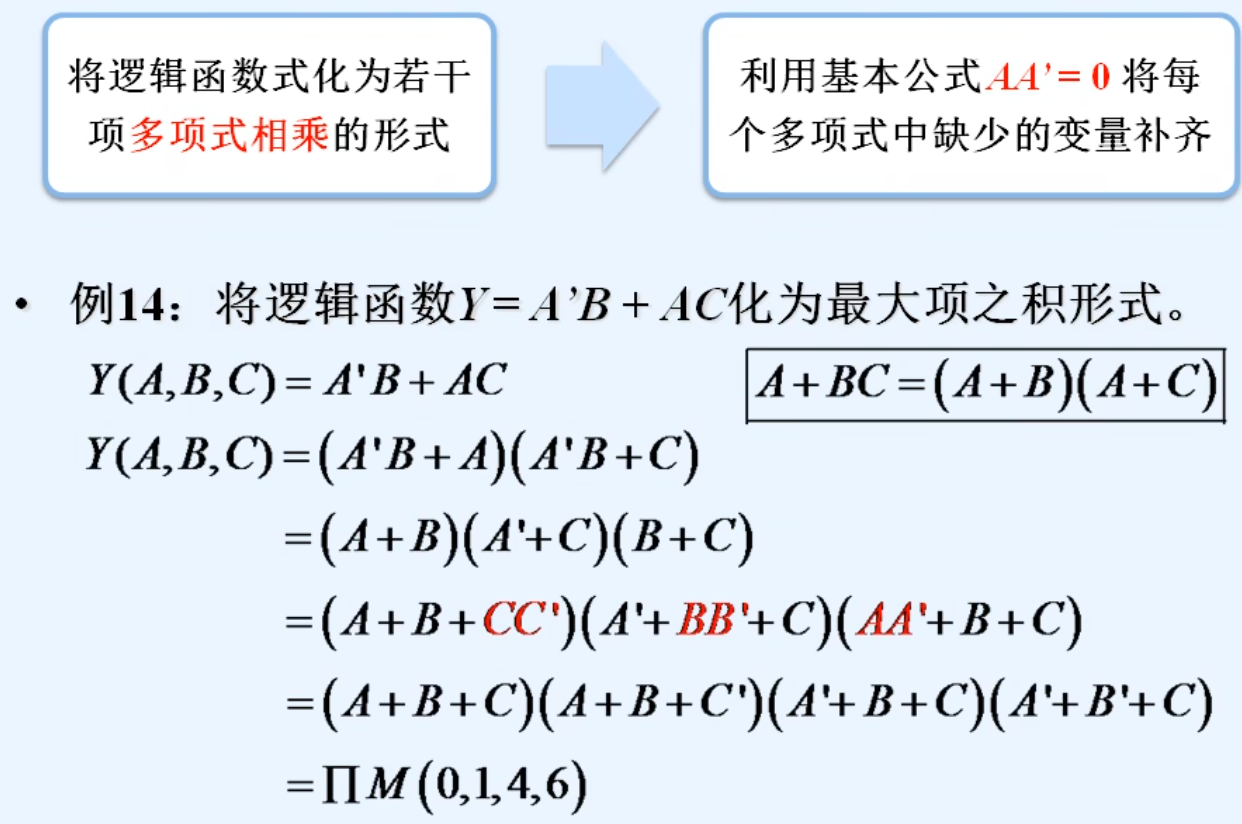
image-20240404212938294

七.逻辑函数的公式化简法

1.最简与或形式

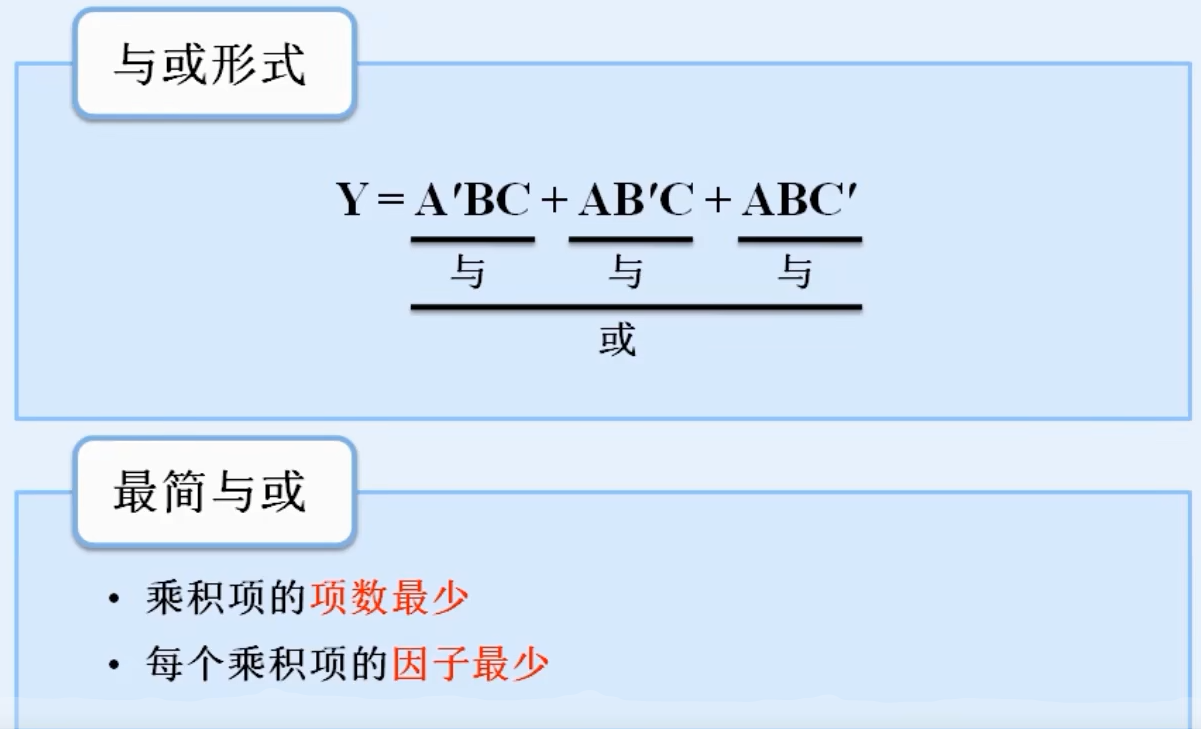
image-20240404213404845

八.最简与或形式的化简方法

image-20240404213454485

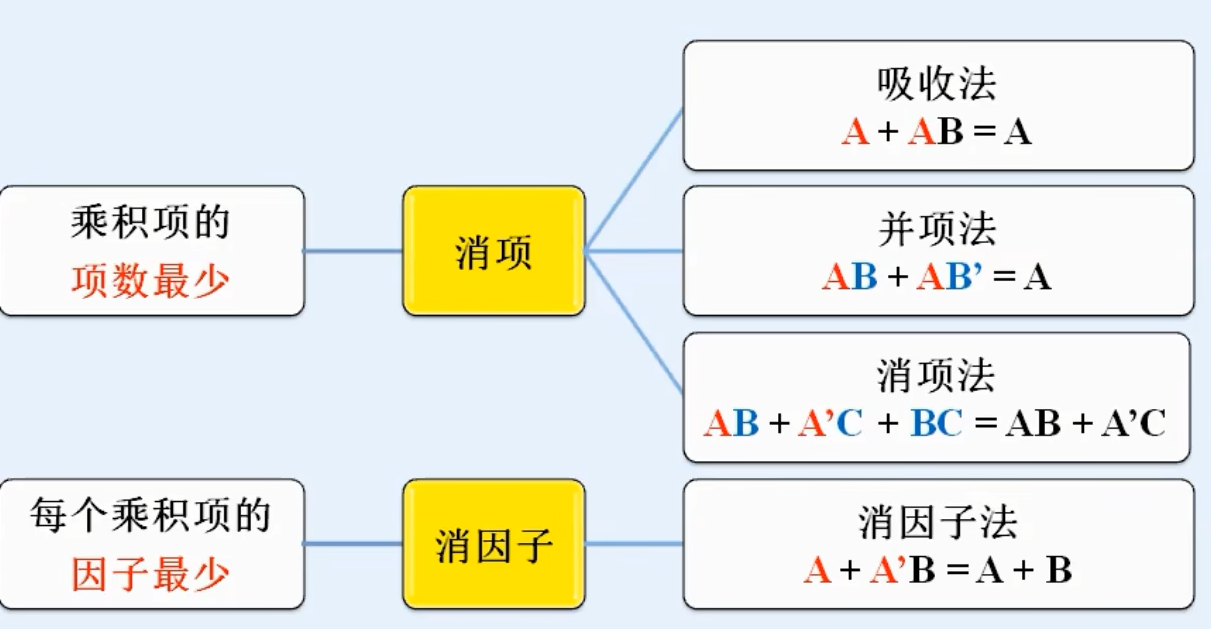
1.公式化简法思路

image-20240404213802163

image-20240404214009127

image-20240404214146600

image-20240404214436615

image-20240404214606796

image-20240404214855268

image-20240404215238216

九.逻辑函数的卡诺图化简法

1.最小项的相邻相消原则

image-20240404215538648

2.用卡诺图表示最小项

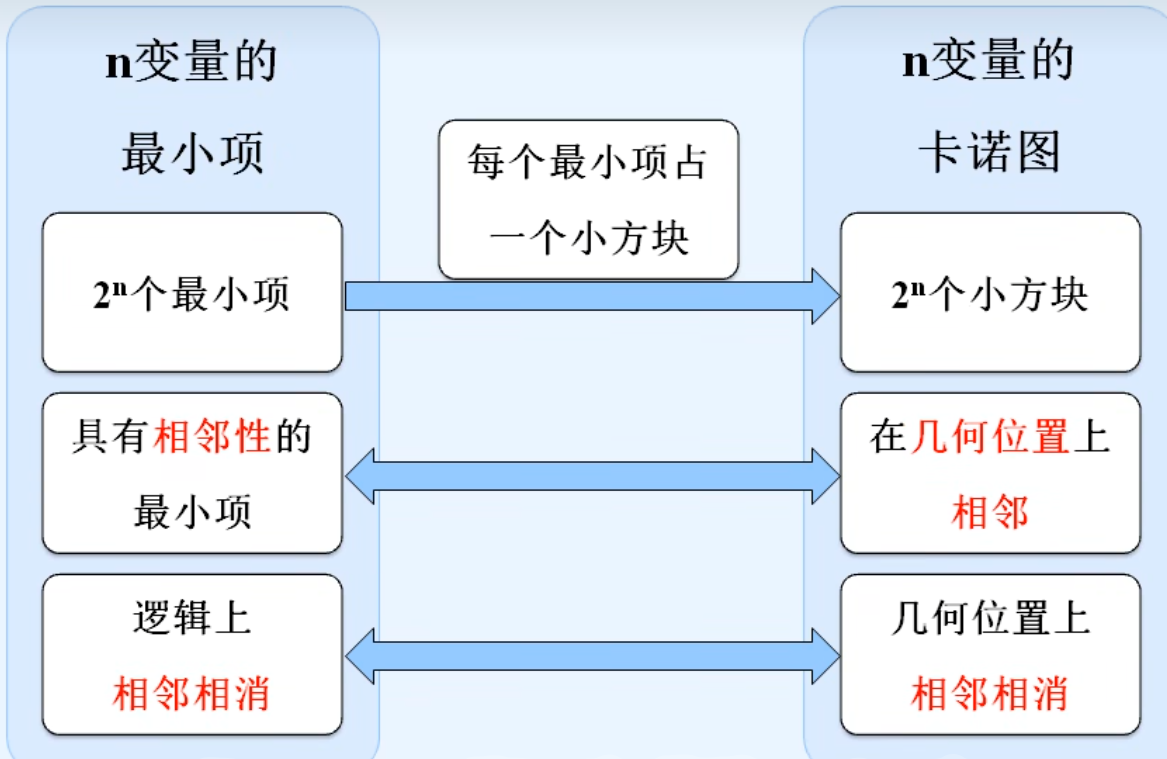
image-20240404215827907

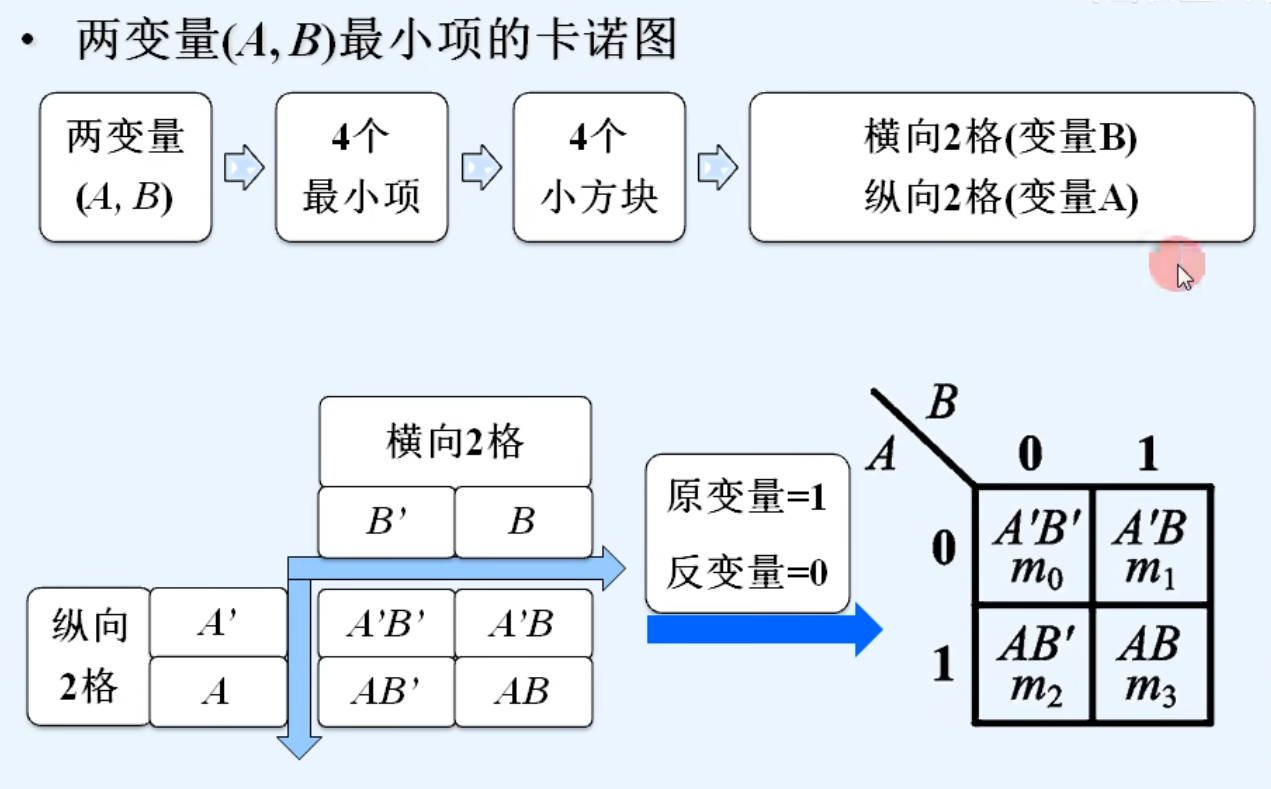
image-20240404220044166

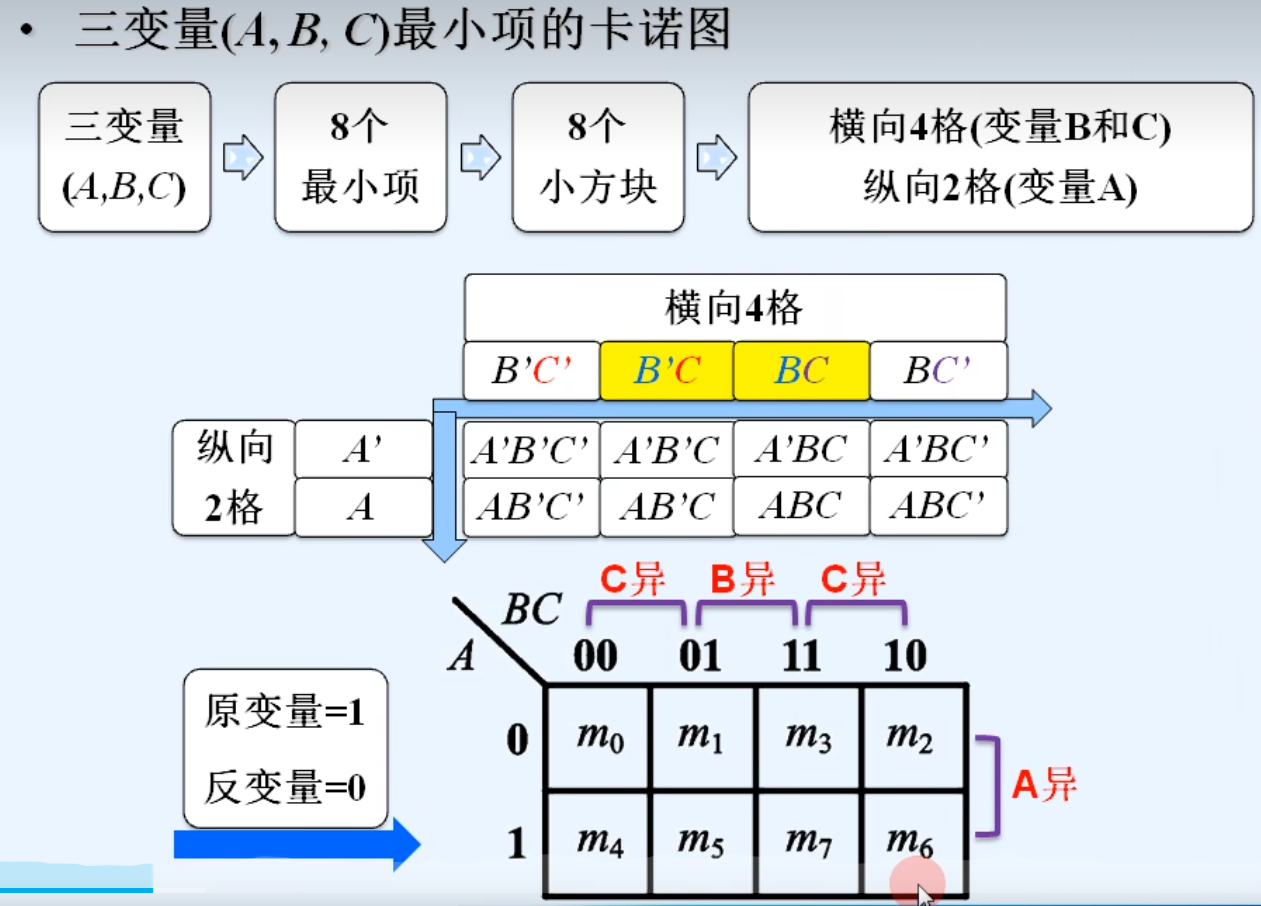
image-20240404220426439

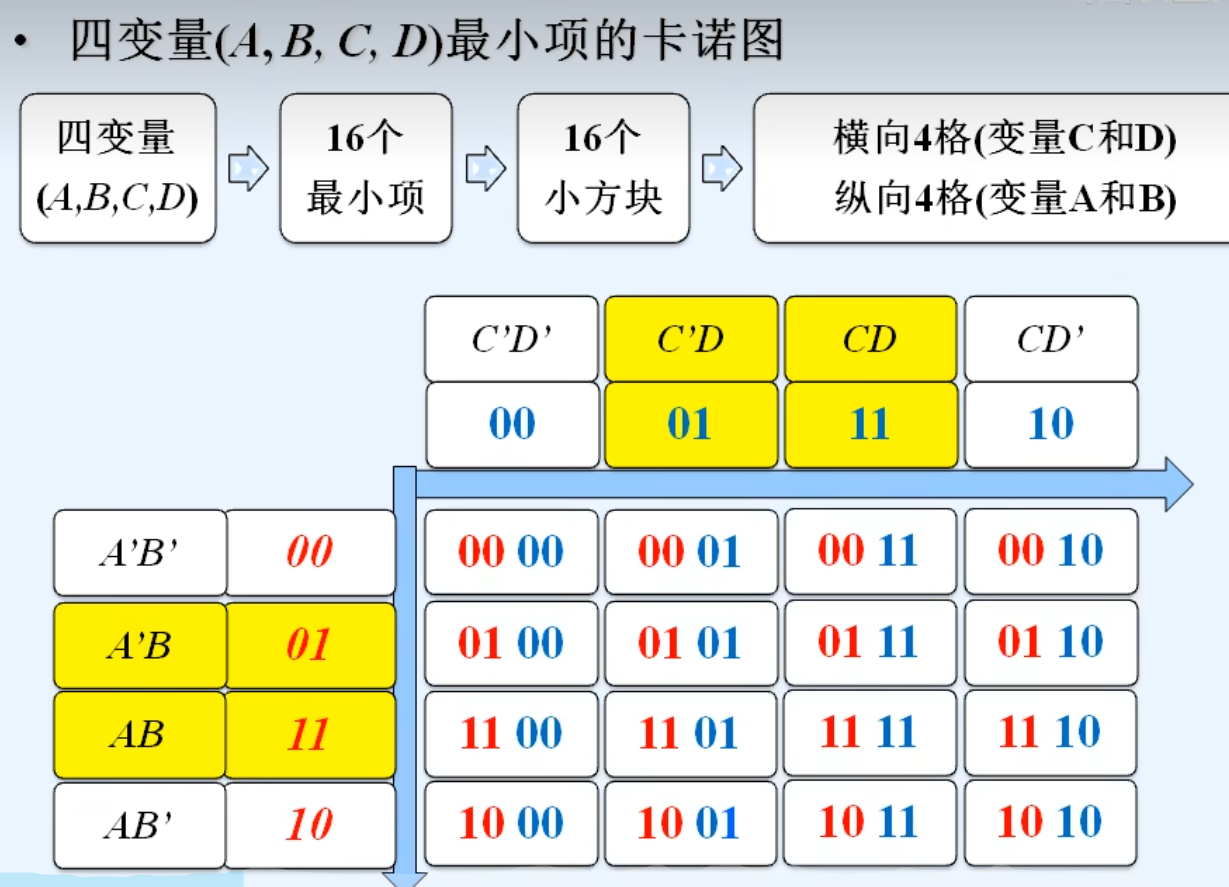
image-20240404220647790

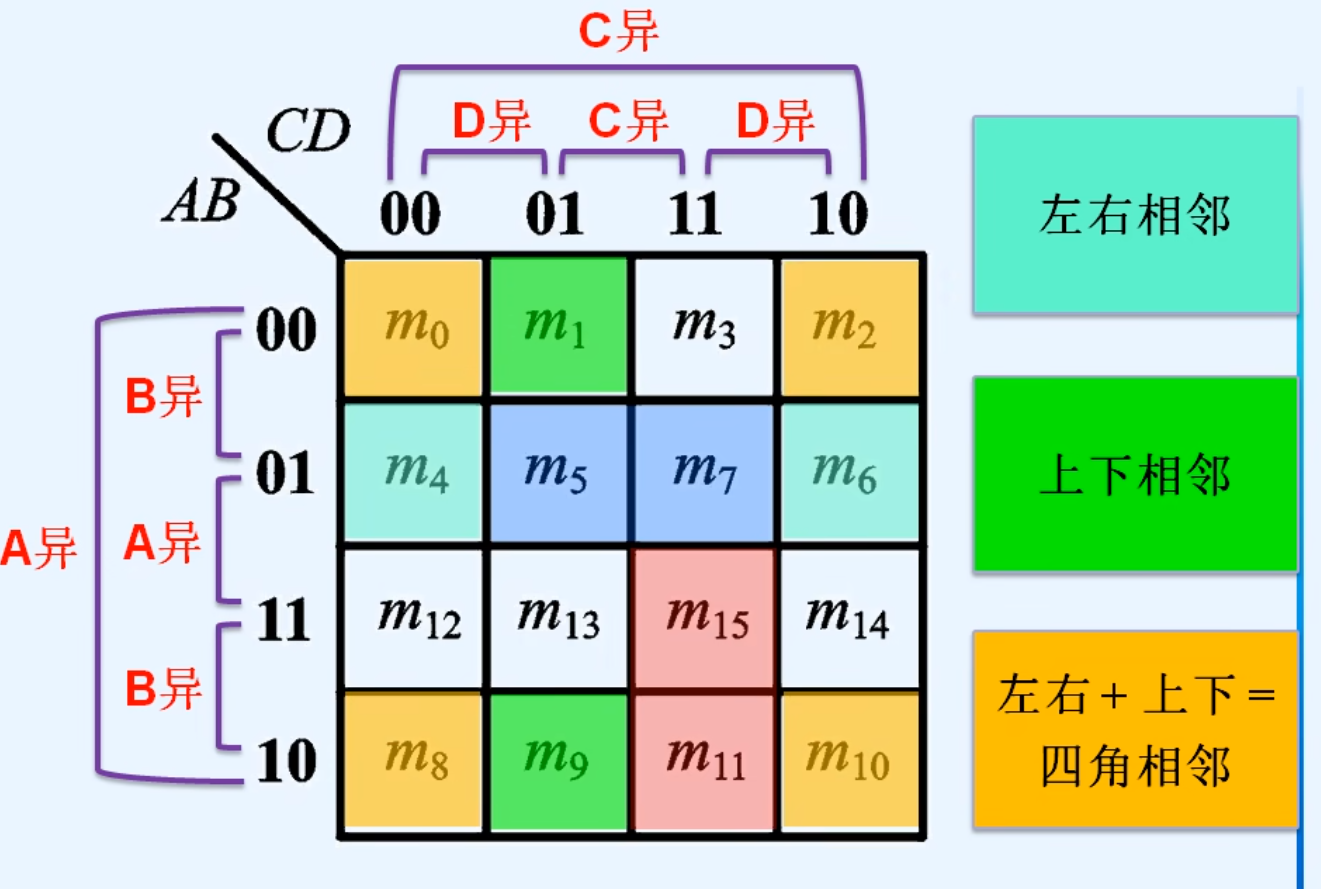
image-20240404221056705

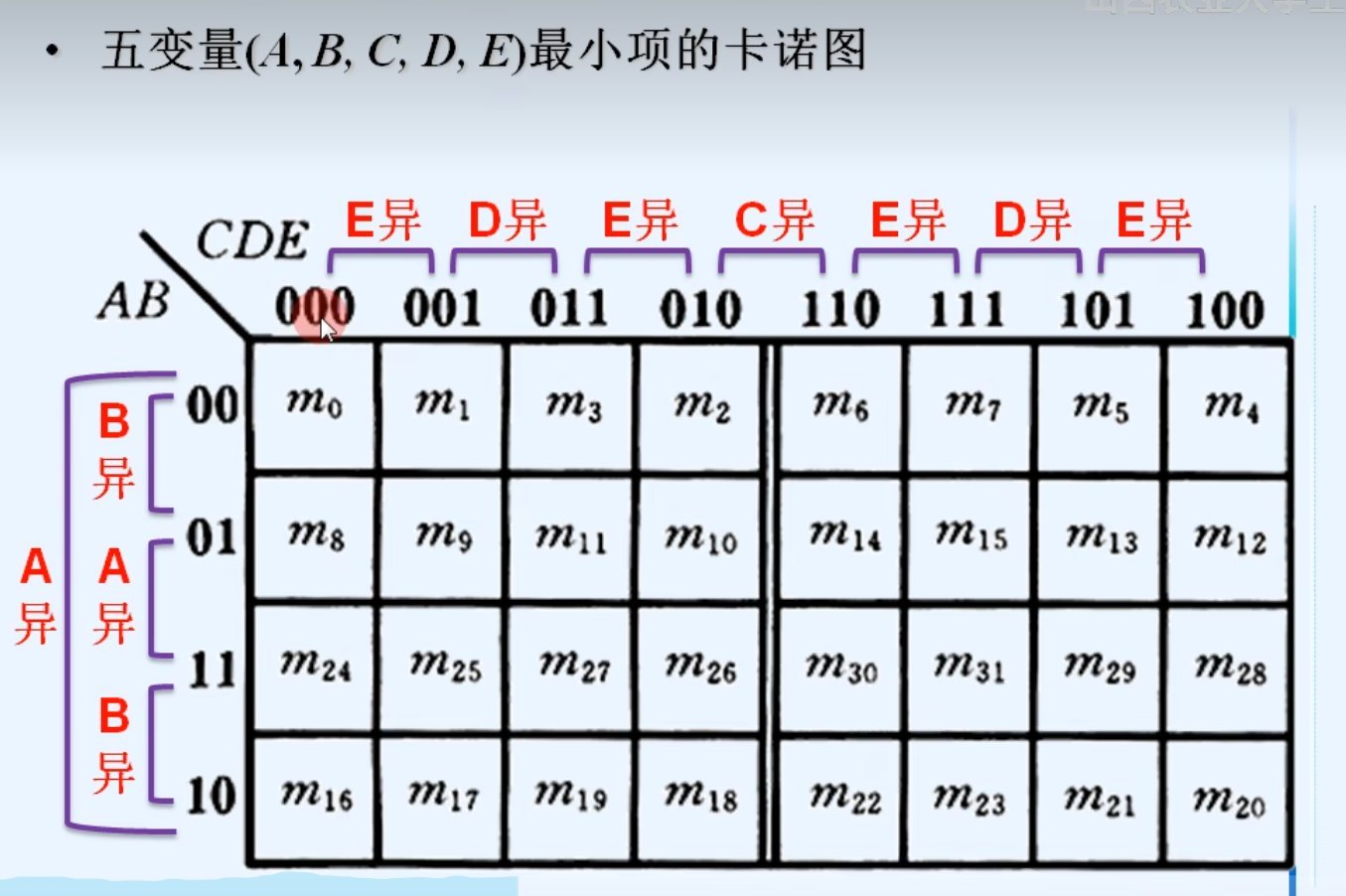
image-20240404221314633

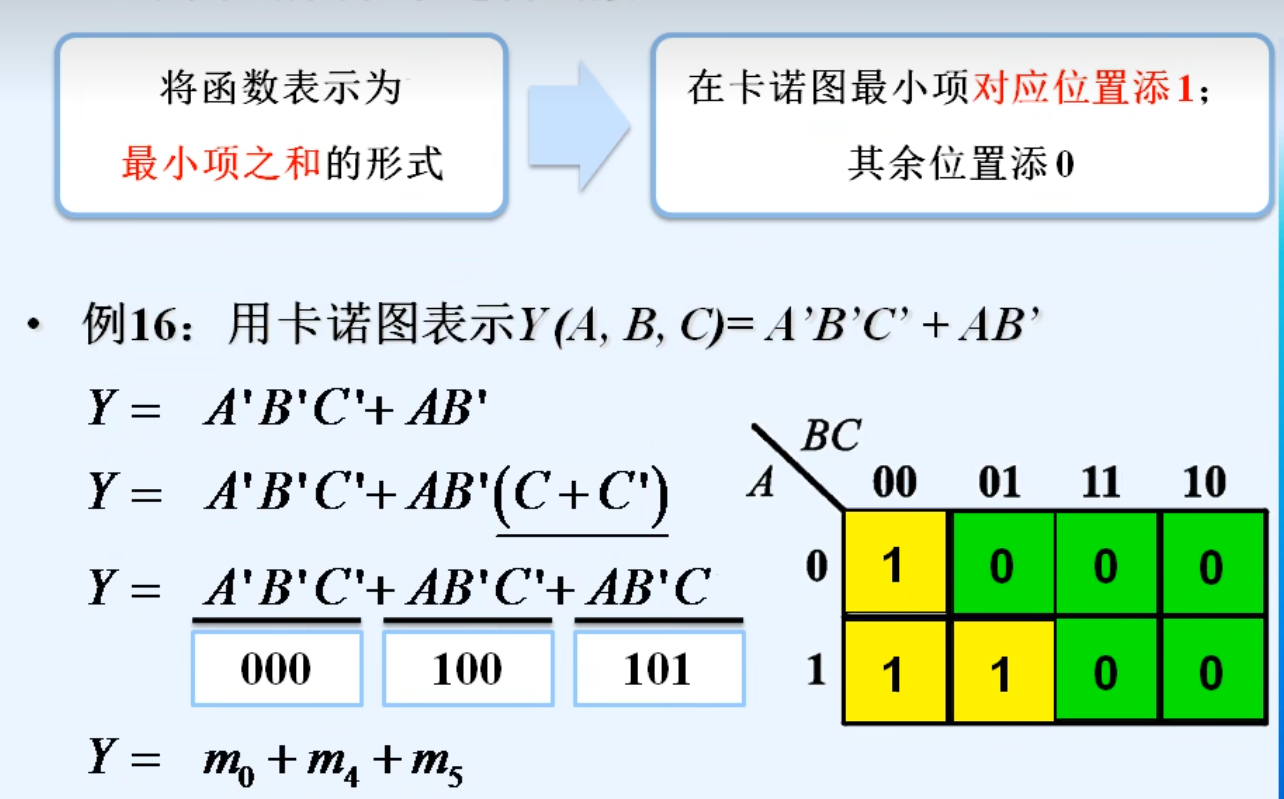
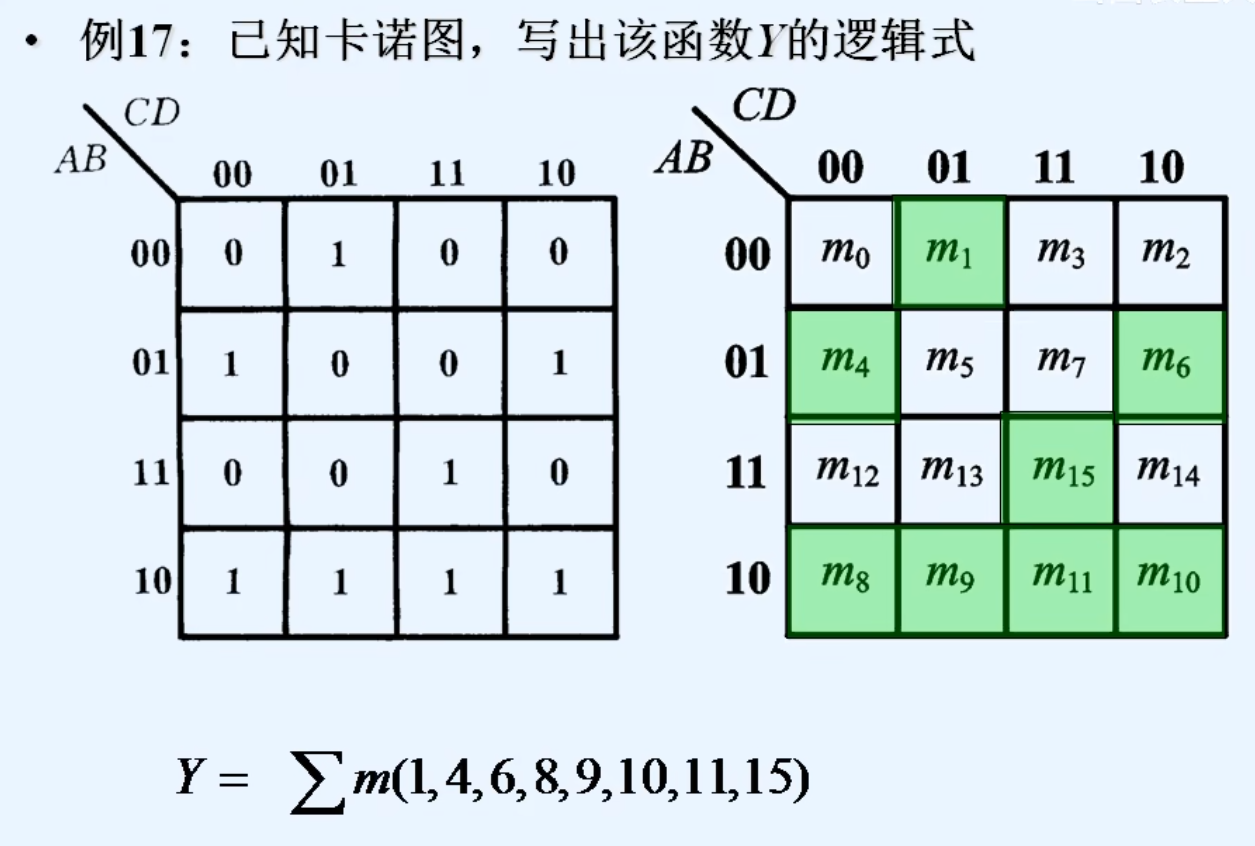
3.用卡诺图表示逻辑函数

image-20240404221607523

image-20240404221740681

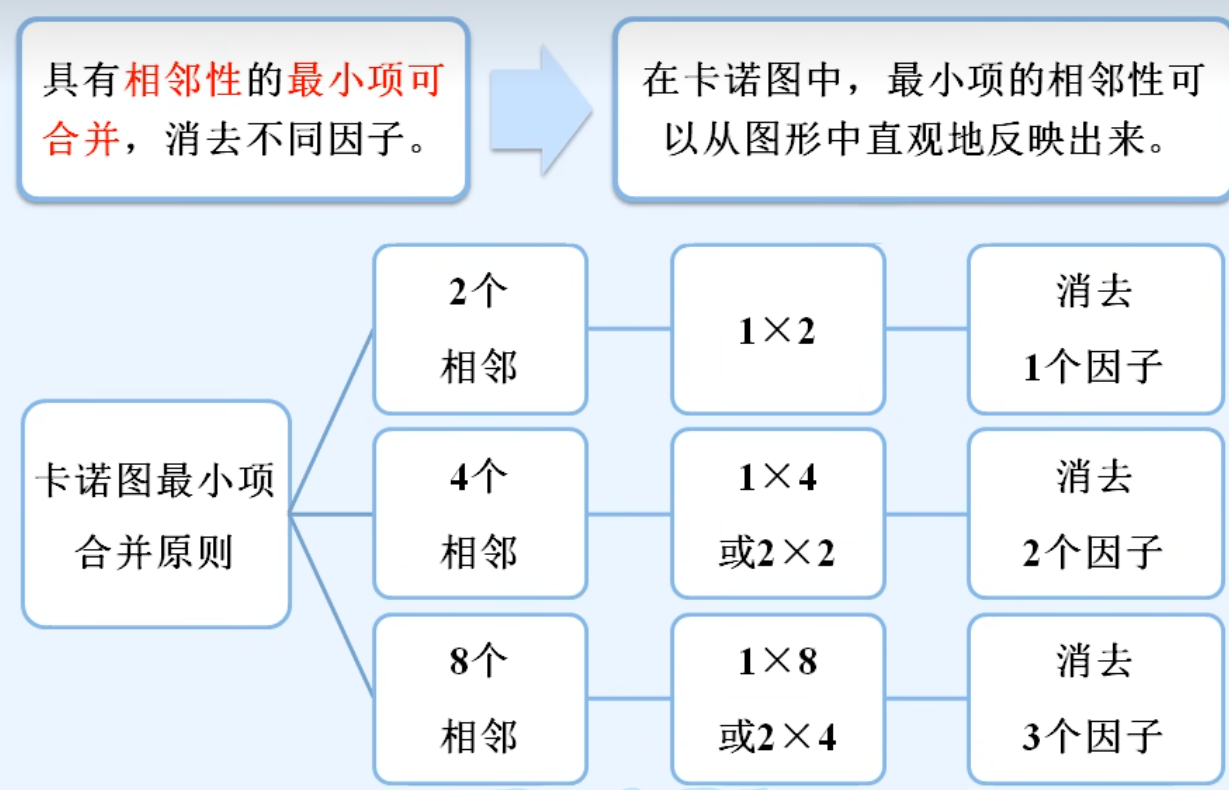
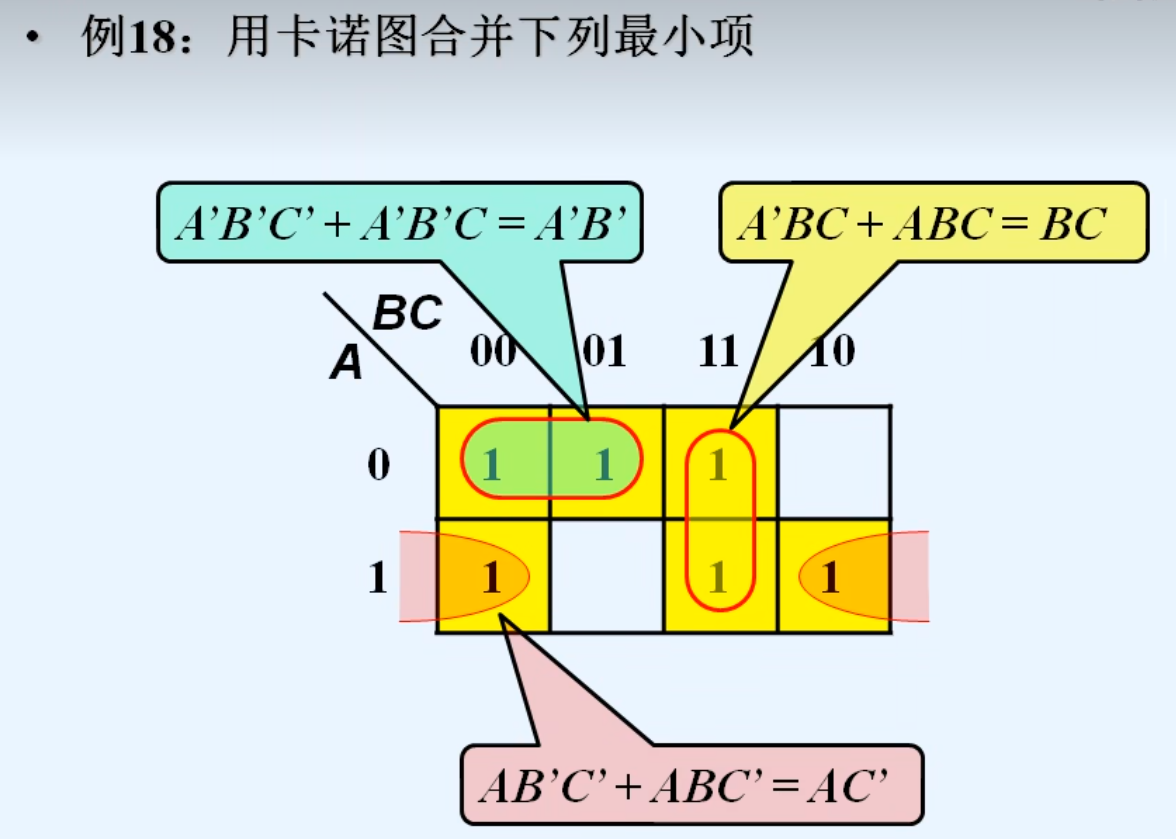
4.卡诺图合并最小项的原则

image-20240404221912690

image-20240404222140360

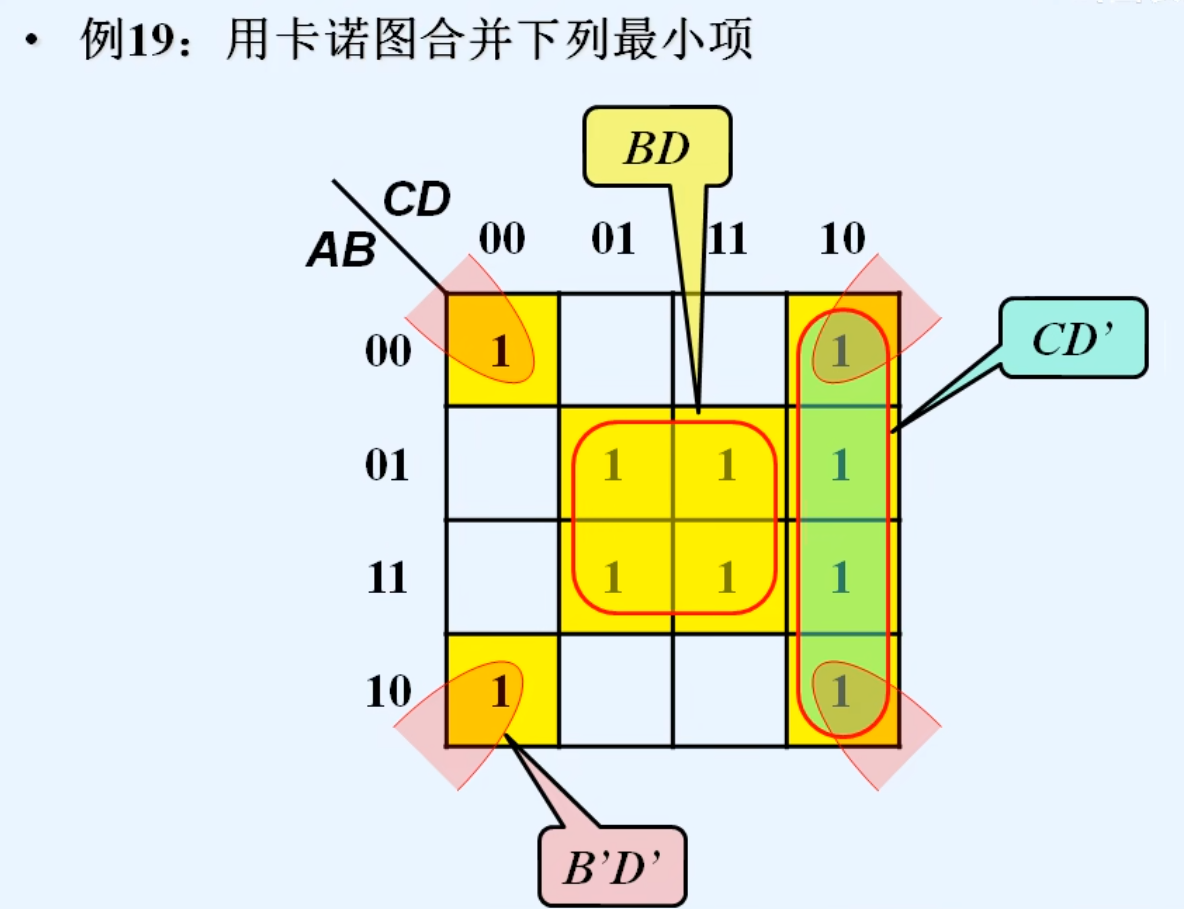
image-20240404222423300

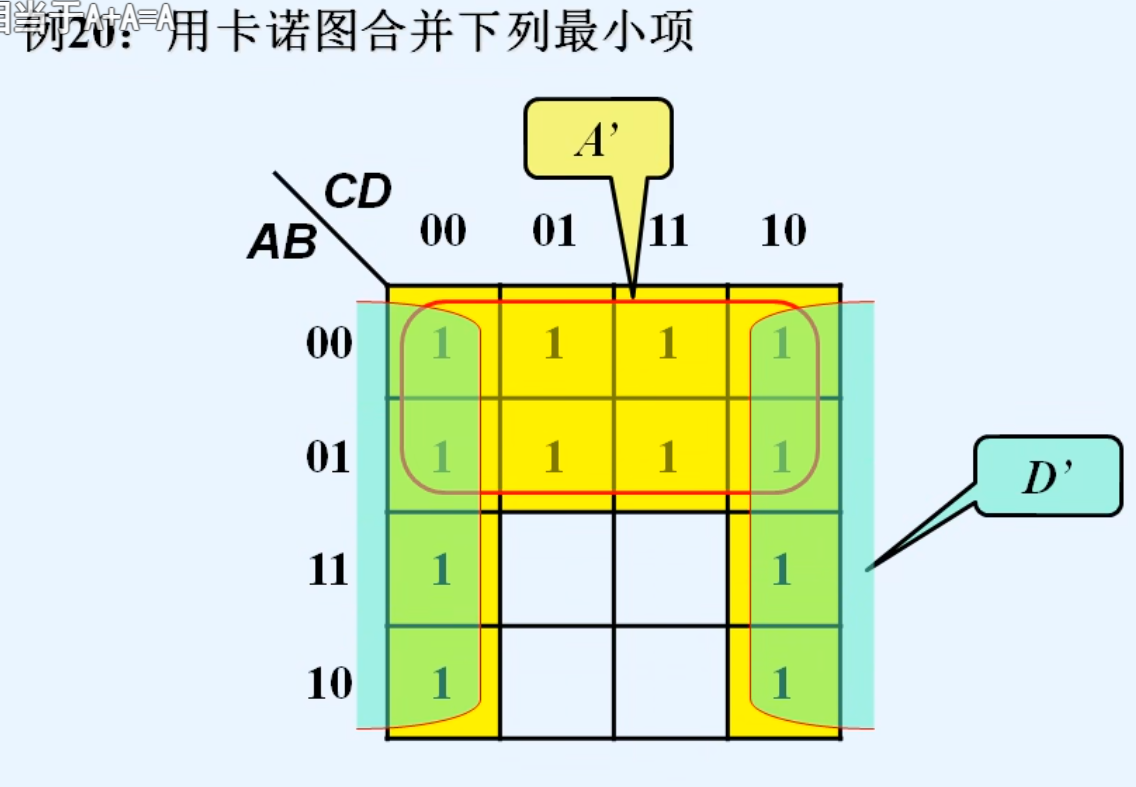
image-20240404222632605

5.卡诺图化简逻辑函数

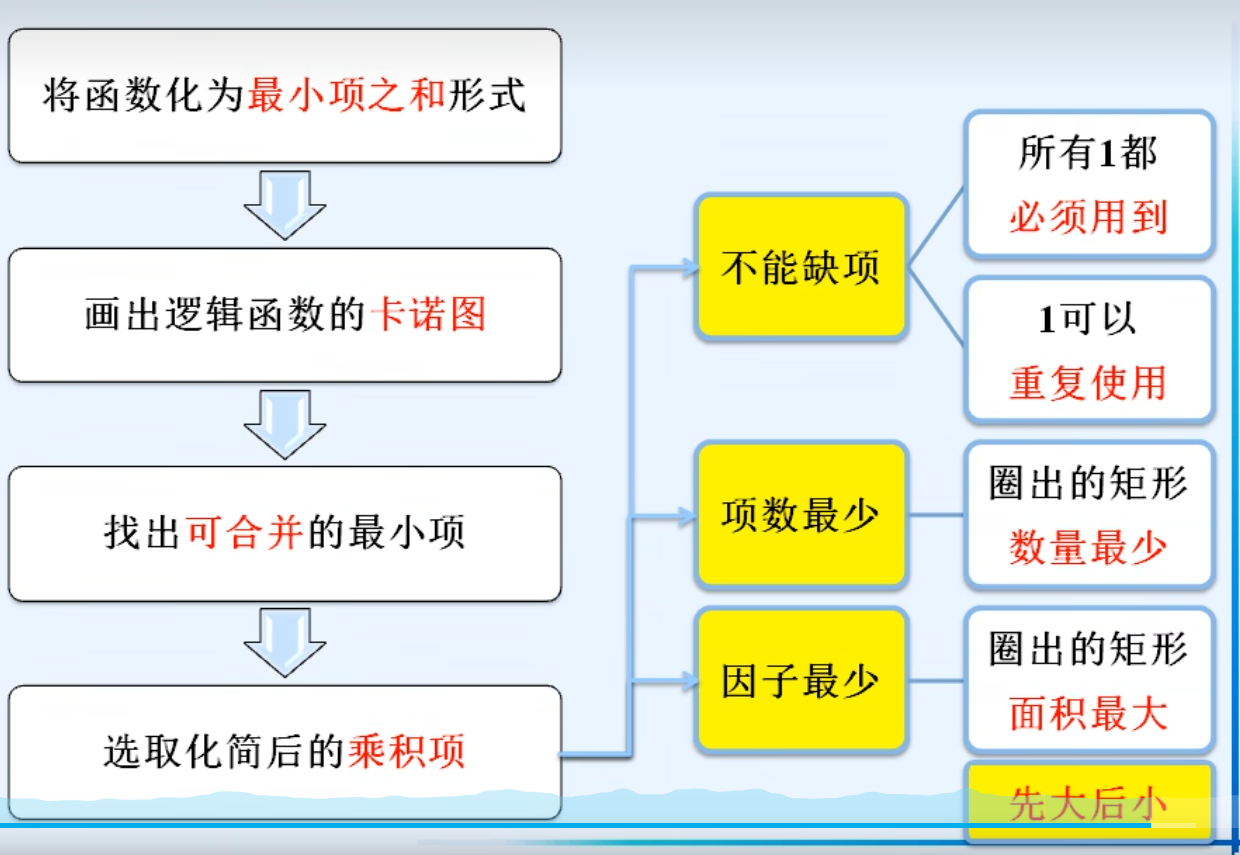
image-20240404222906467

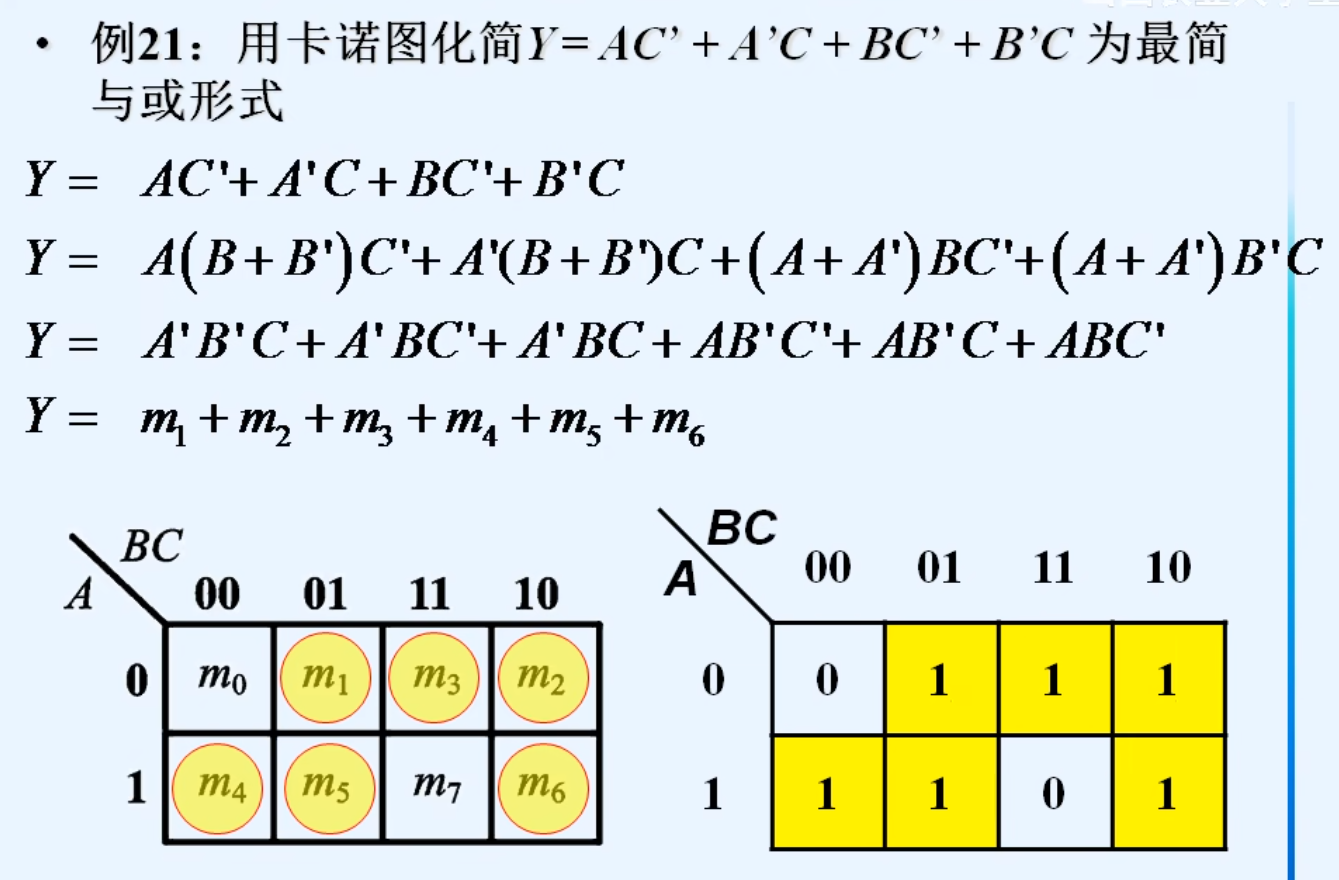
image-20240404225619719

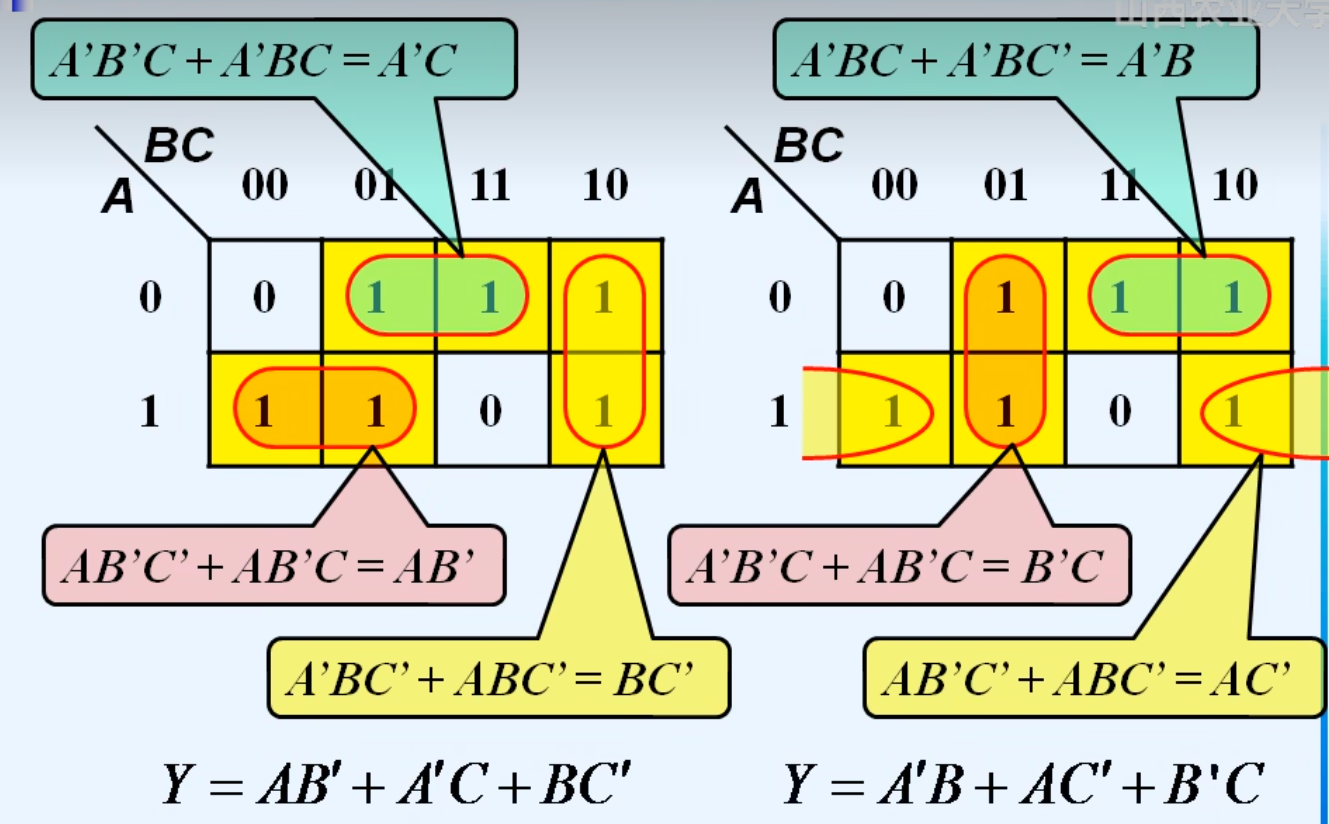
image-20240404225838957

同一逻辑函数的化简结果并不一定唯一

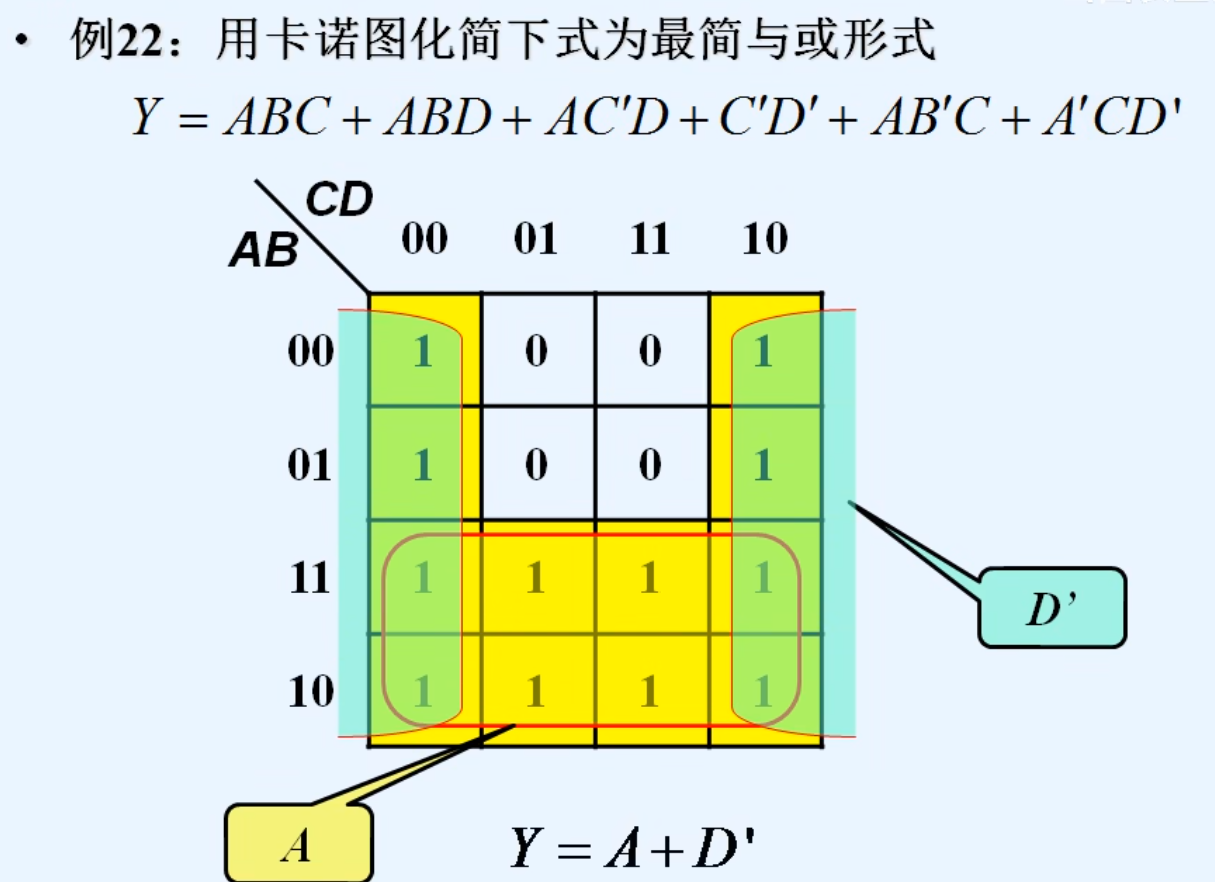
image-20240404230324546

十.具有无关项及多输出逻辑函数的化简

1.无关项

image-20240404231129952

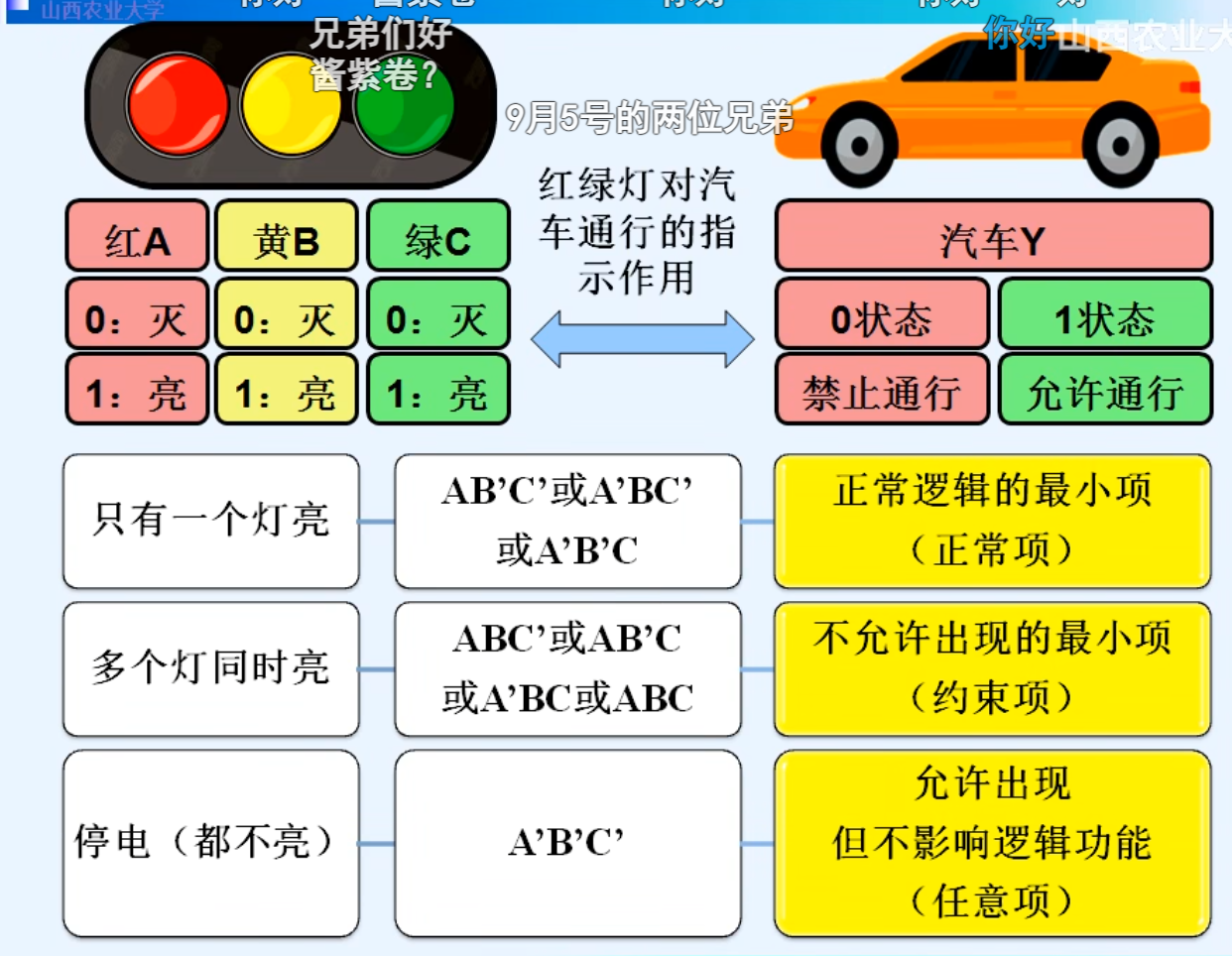
image-20240404231432096

image-20240404231959461

2.利用无关项化简逻辑函数

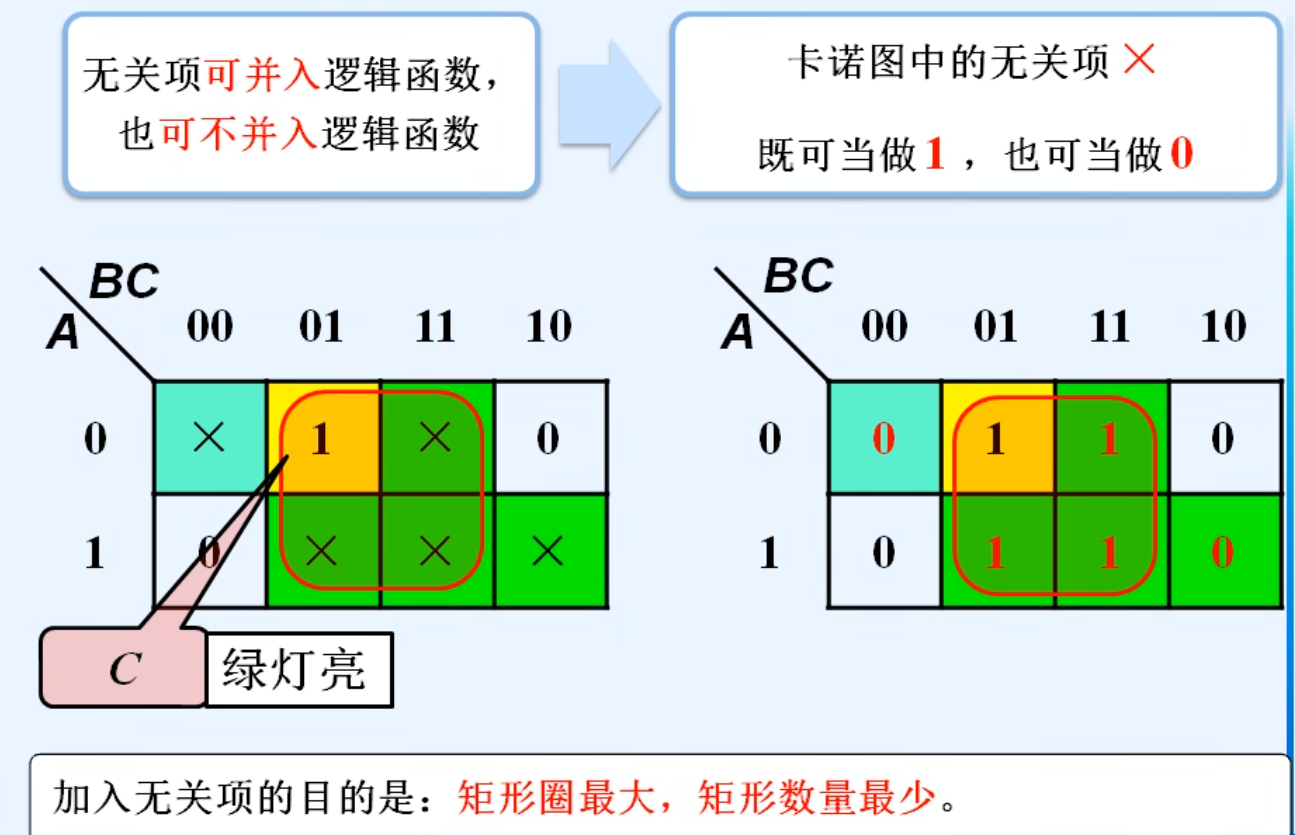
image-20240404232144245

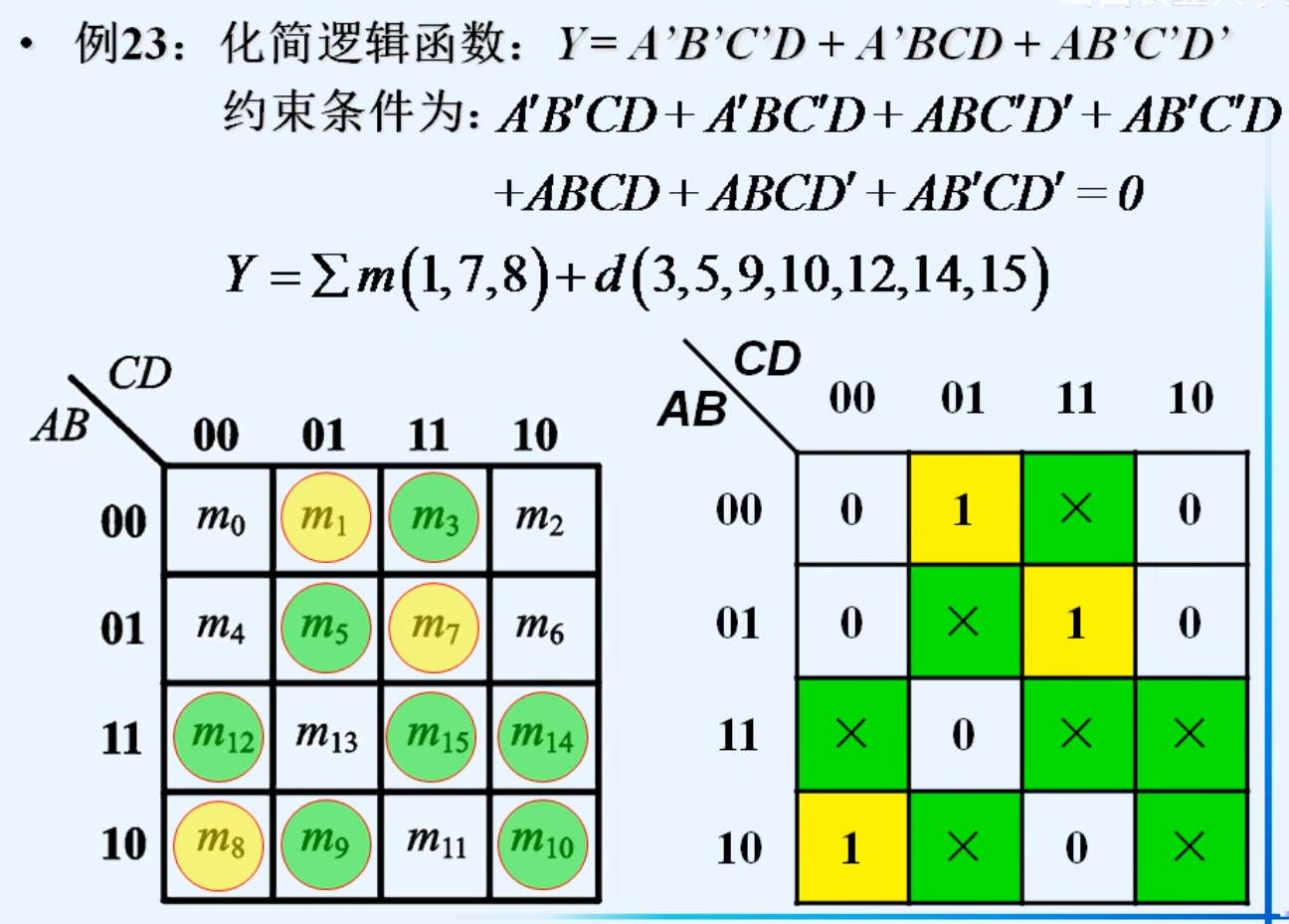
image-20240404232357539

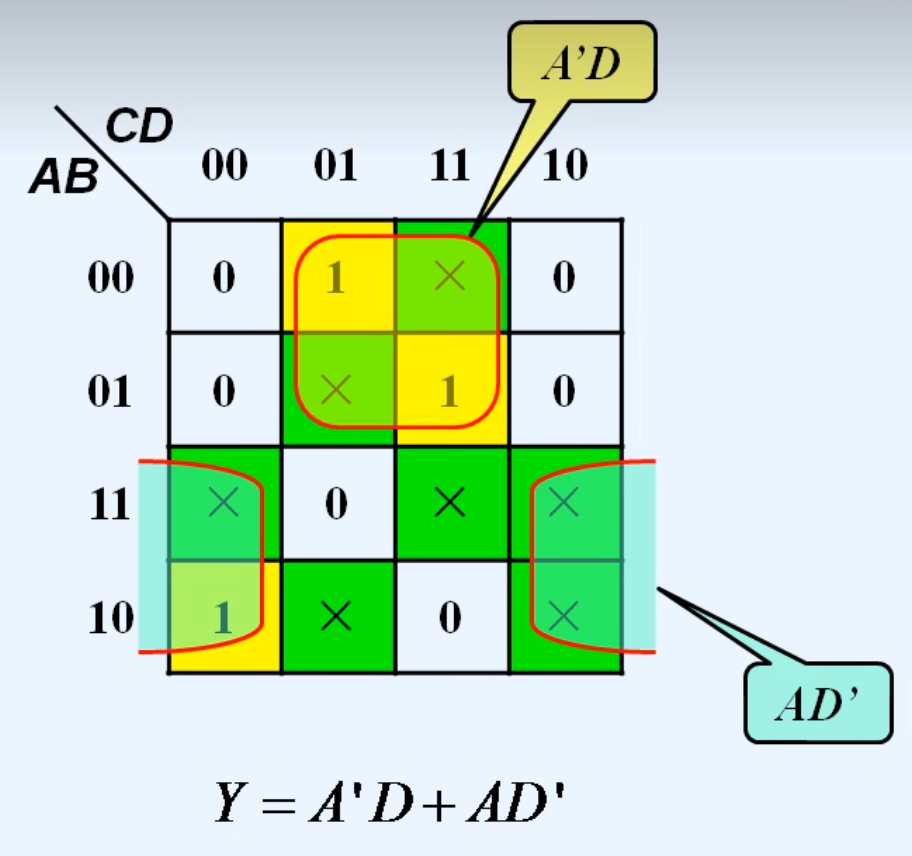
image-20240404232700765

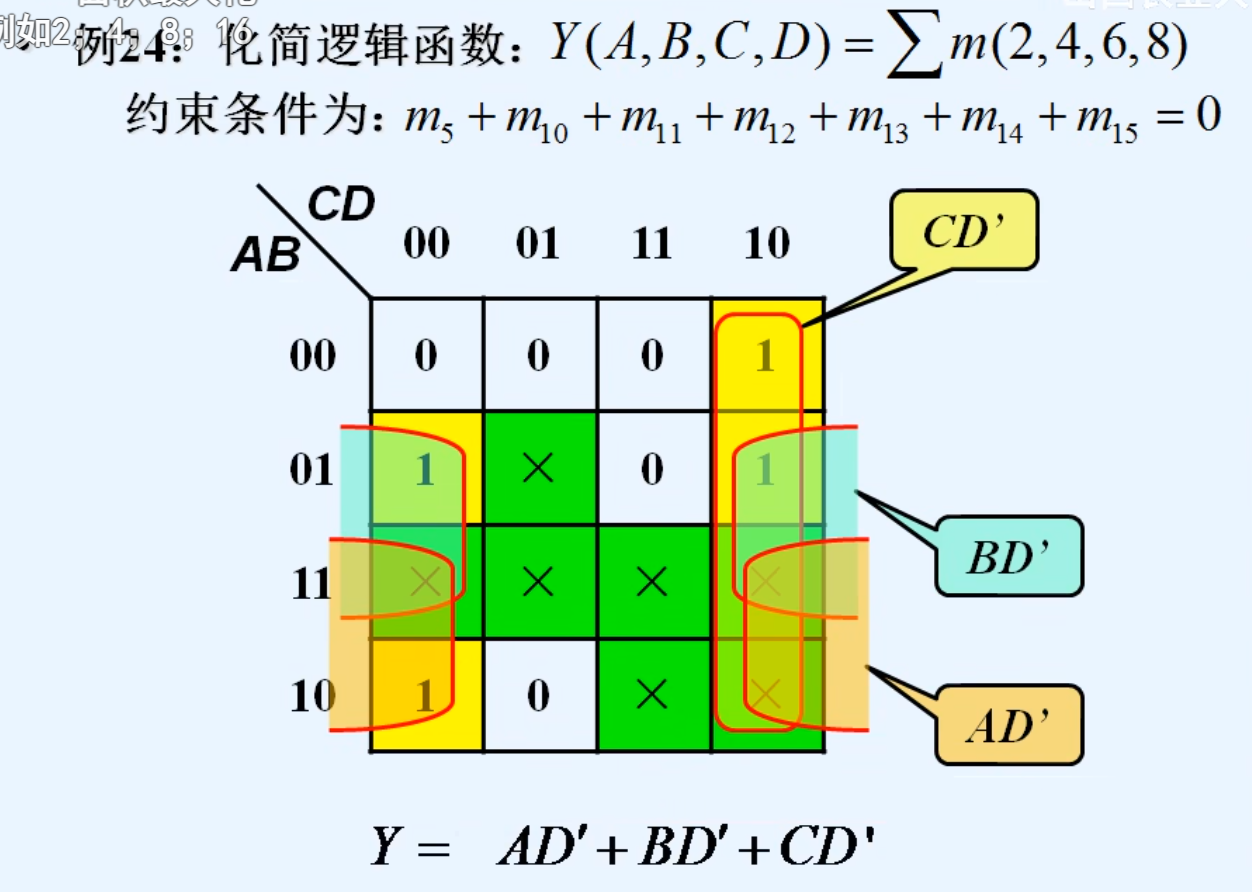
image-20240404233048317

十一.多输出逻辑函数的化简

image-20240404233130898

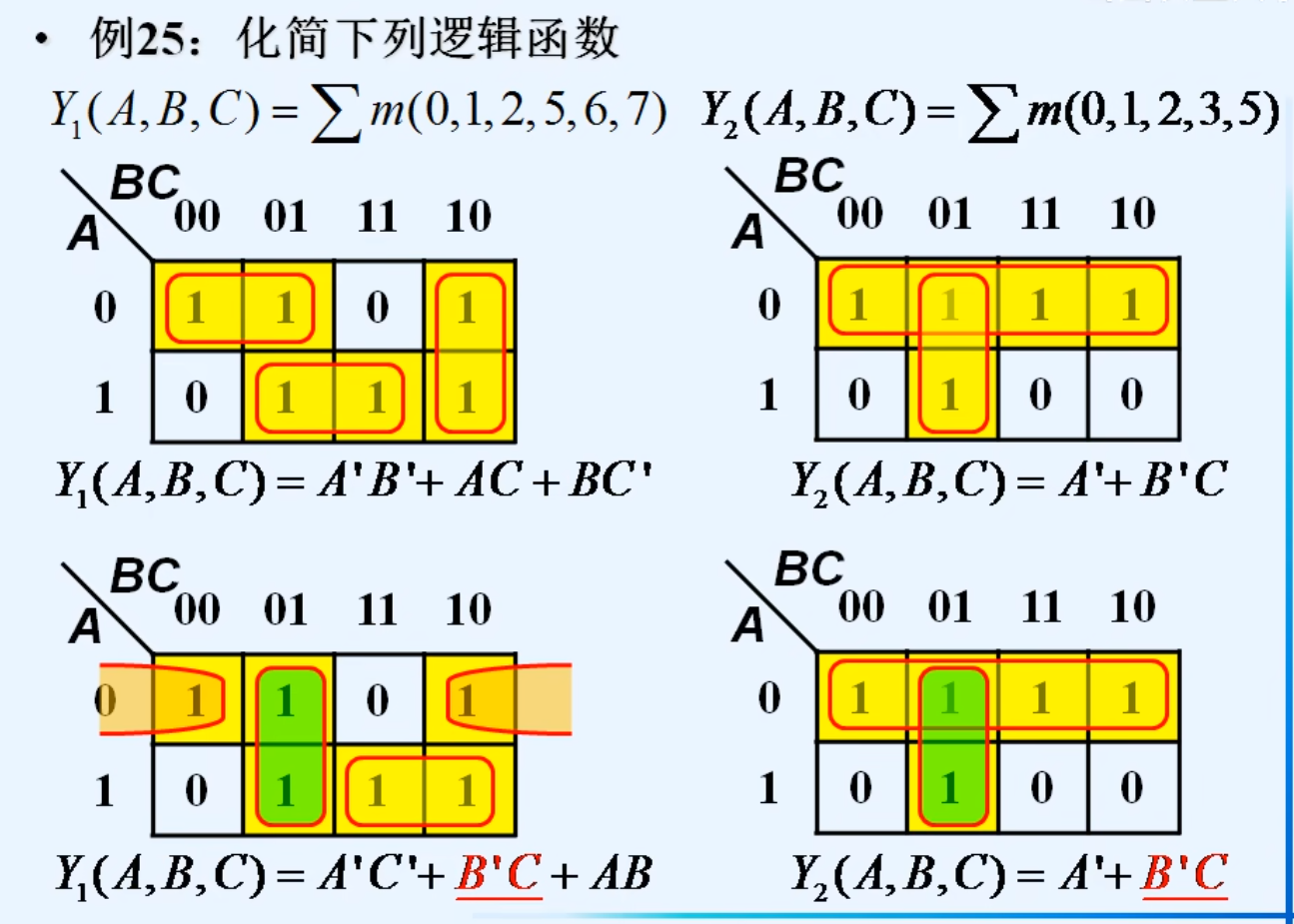
image-20240404233421741

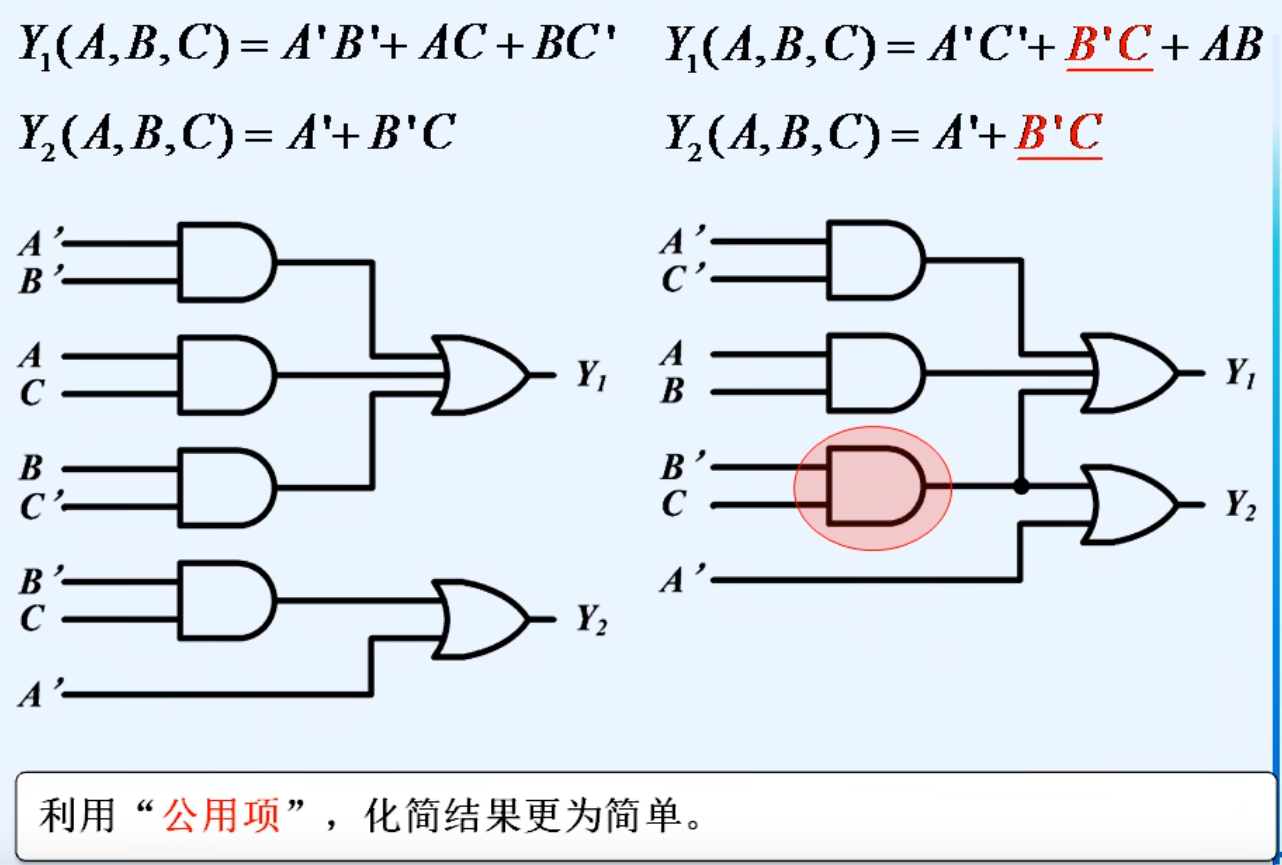
image-20240404233604972

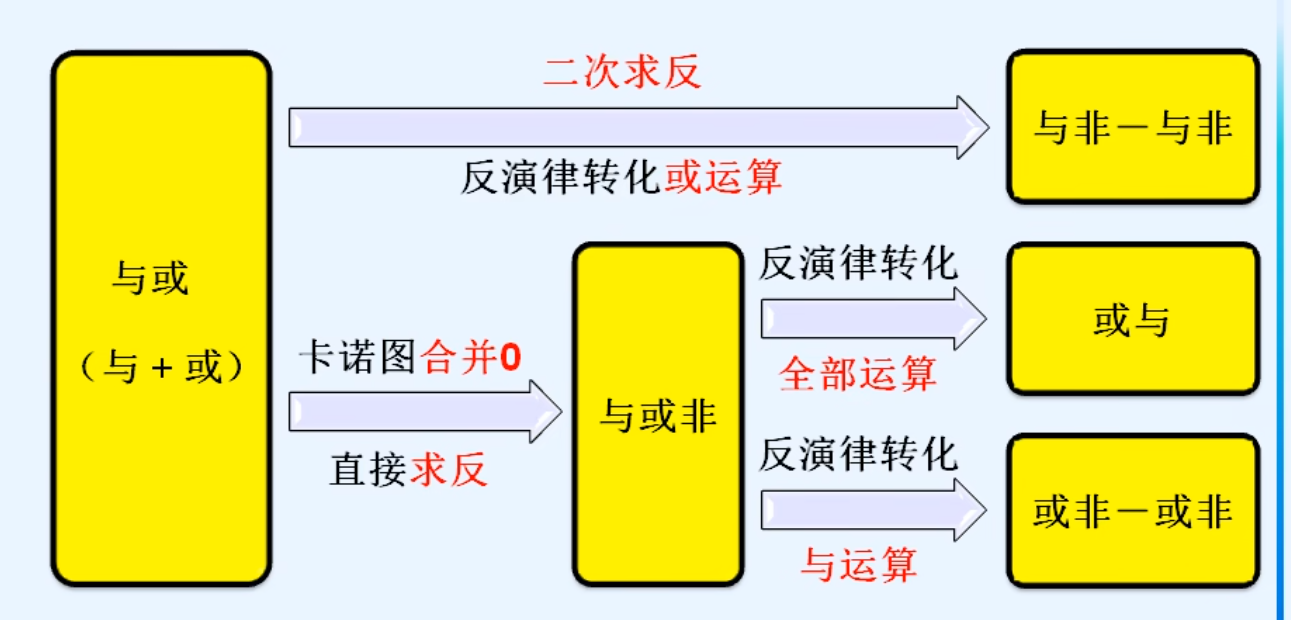
十二.逻辑函数形式的变换

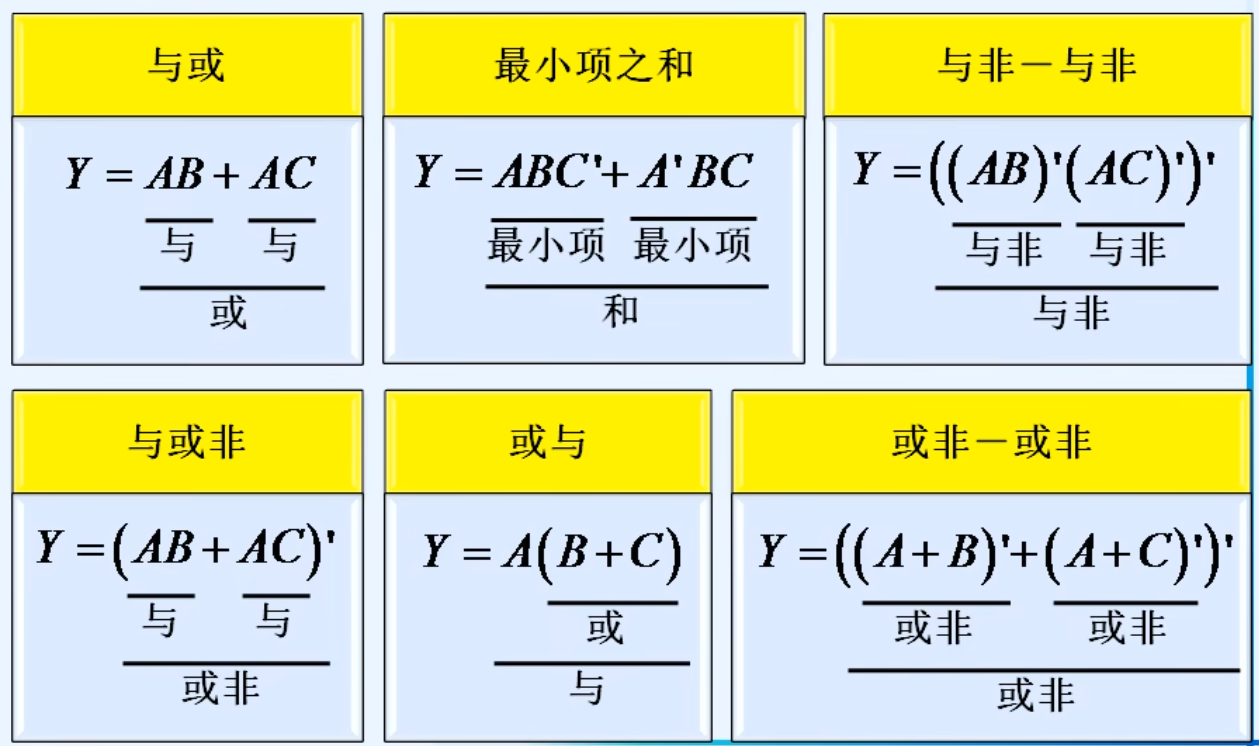
1.常用逻辑函数形式

image-20240404234312765

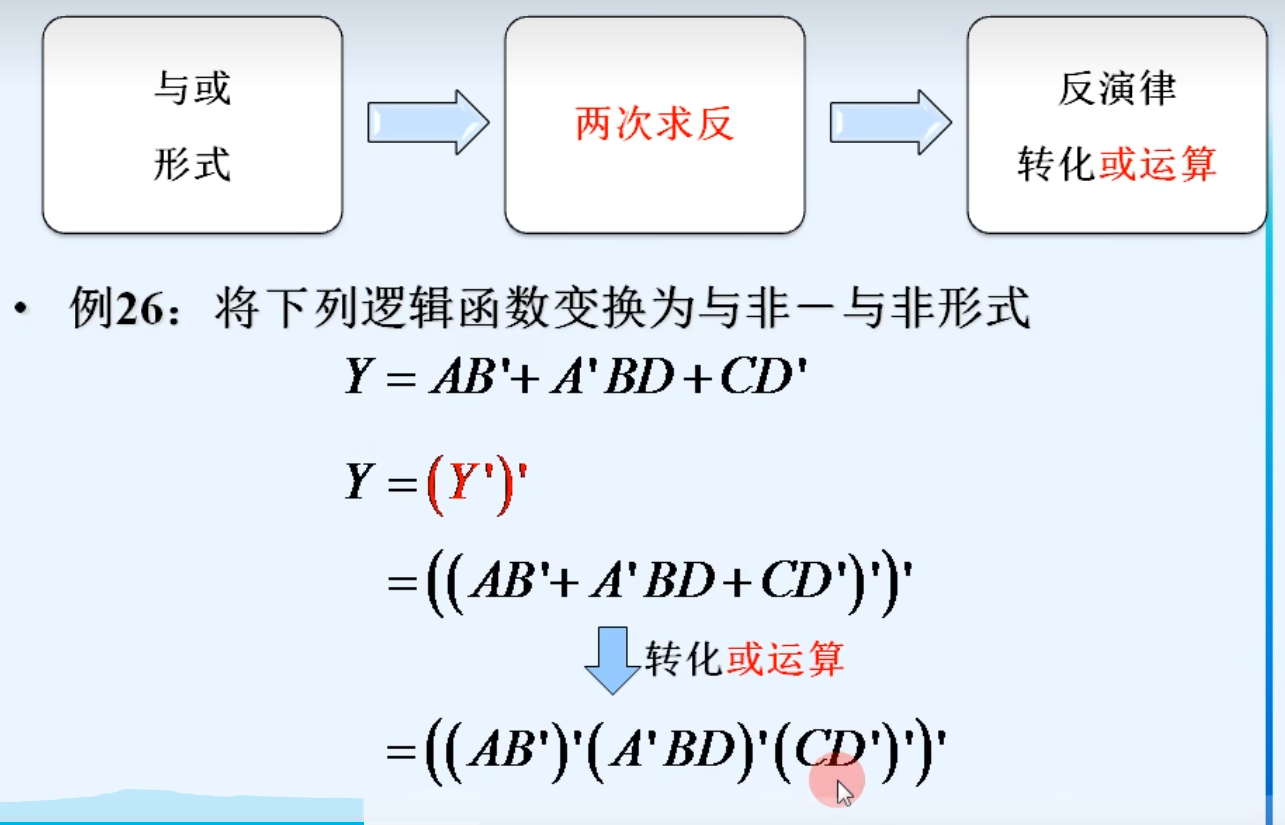
2.与非-》与非-与非

image-20240404234739912

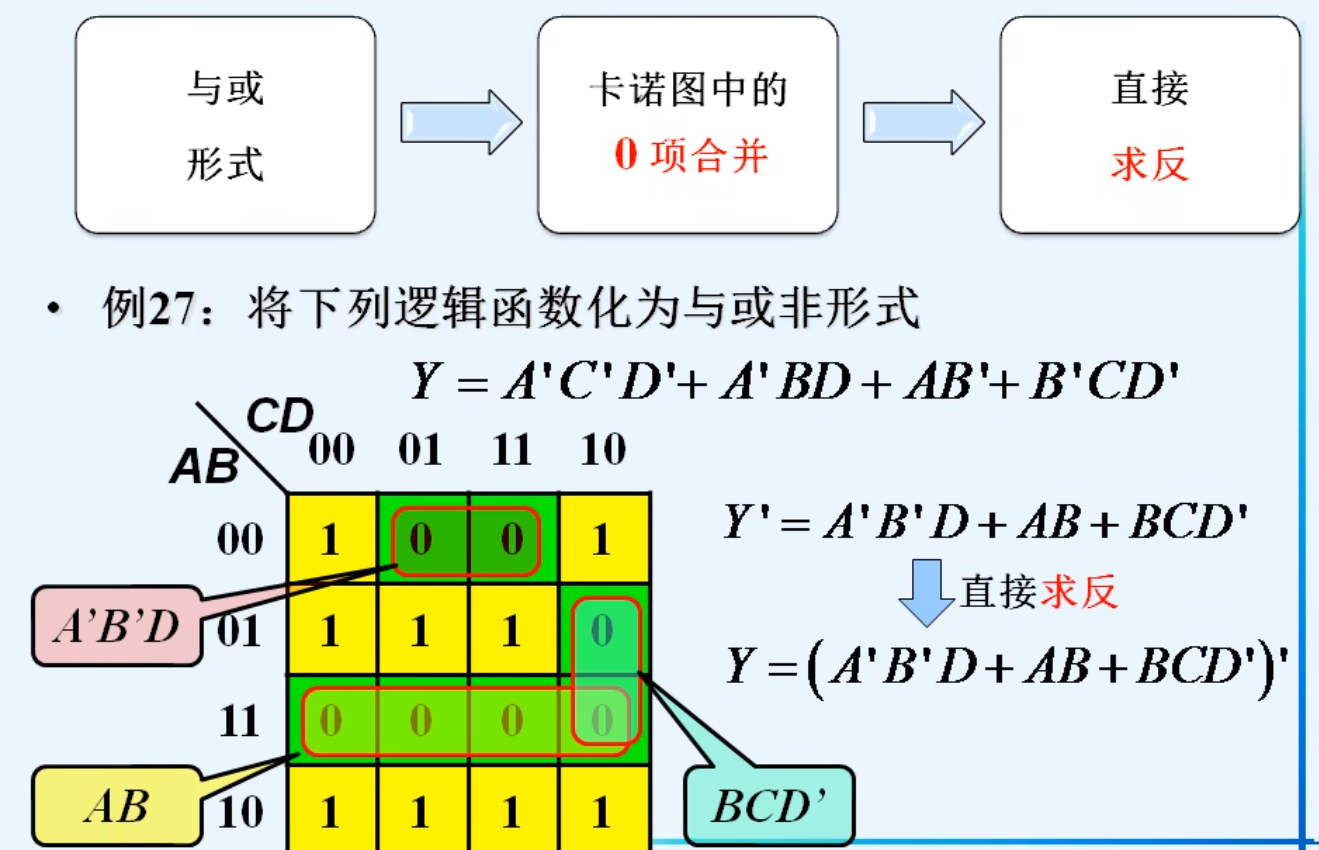
3.与或-》与或非

image-20240404235032605

4.与或-》或与

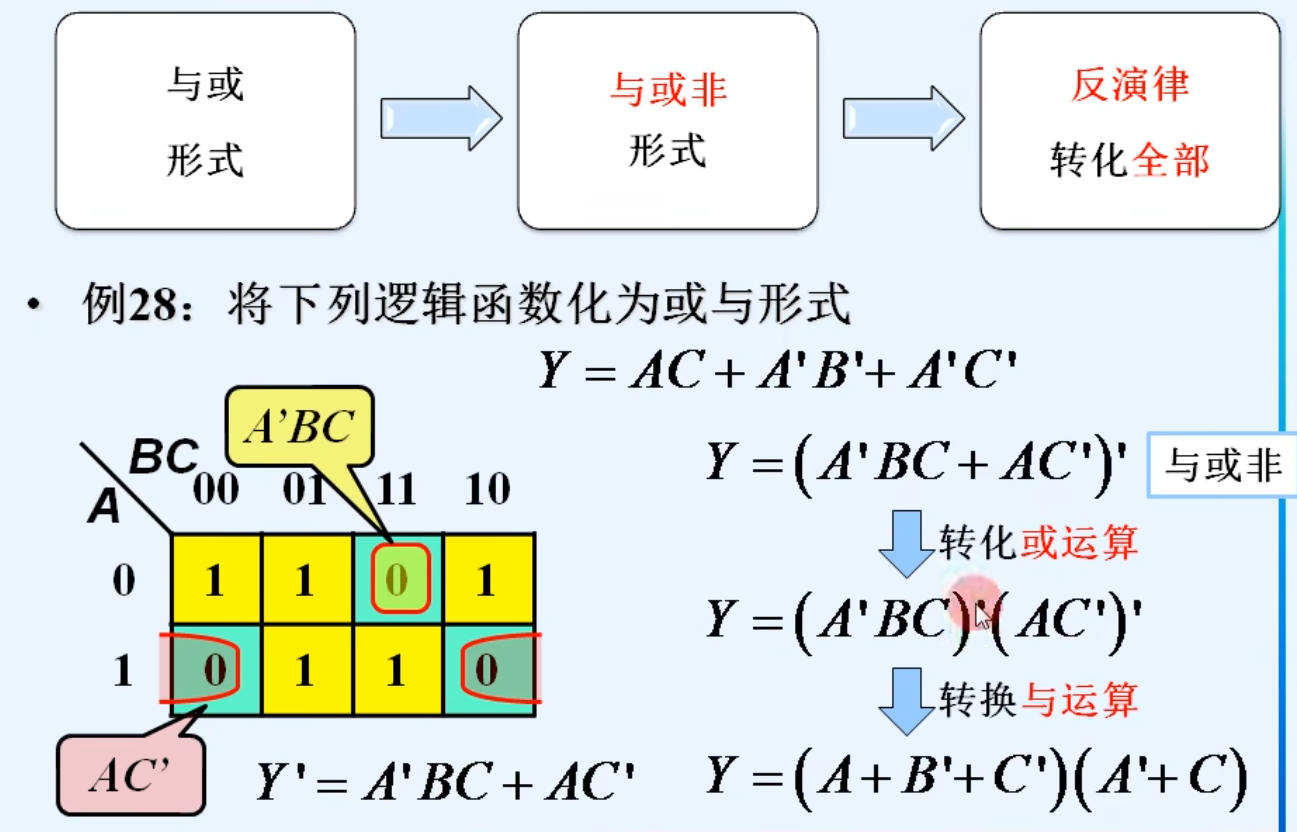
image-20240404235308519

5.与或-》或非-或非

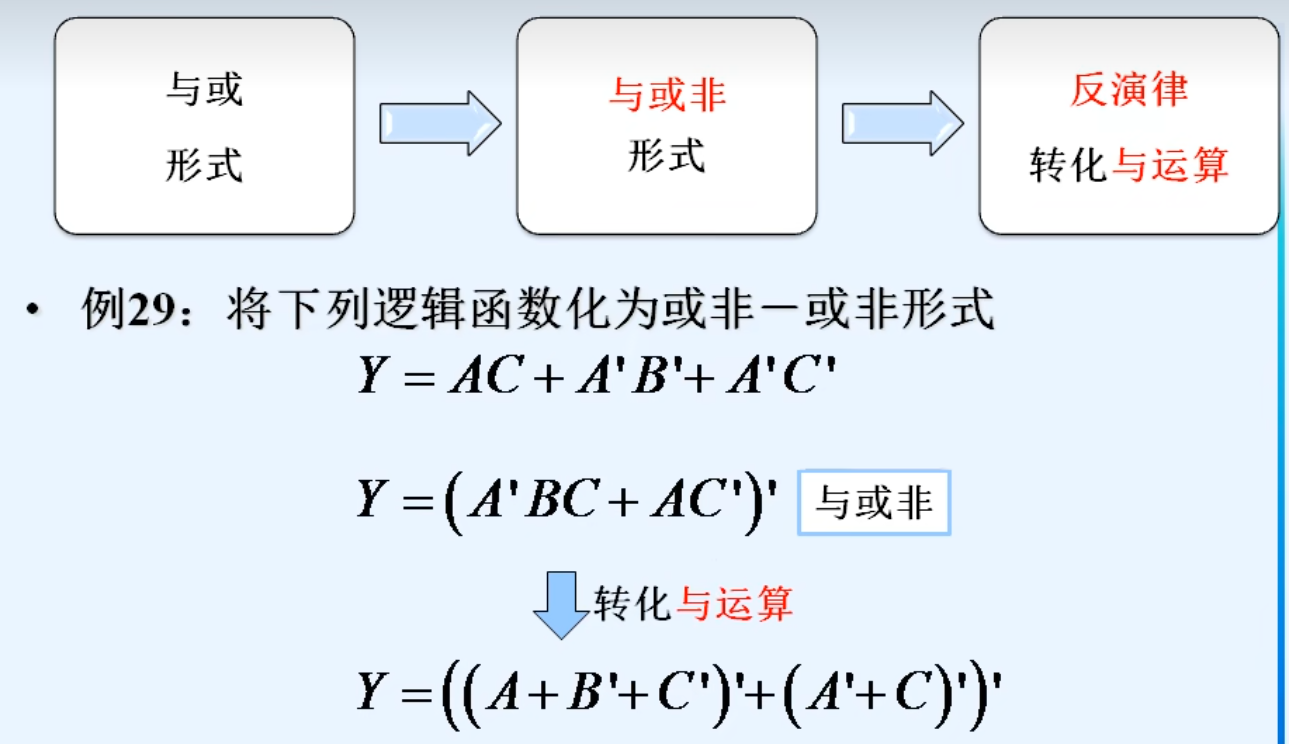
image-20240404235754960

6.逻辑函数形式的变化总结

image-20240405000039256